Cho hàm số y=/x/ +/1-x/
a) vẽ đồ thị hàm số
b) dùng đồ thị tìm GTLN của y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=\left|x+1\right|+\sqrt{\left(x-2\right)^2}=\left|x+1\right|+\left|x-2\right|\)
\(\Rightarrow\left\{{}\begin{matrix}y=2x-1\text{ với }x\ge2\\y=1-2x\text{ với }x\le-1\\y=3\text{ với }-1\le x\le2\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau (vẽ 3 đồ thị hàm bậc nhất xác định trên trên ở từng khoảng của chúng)
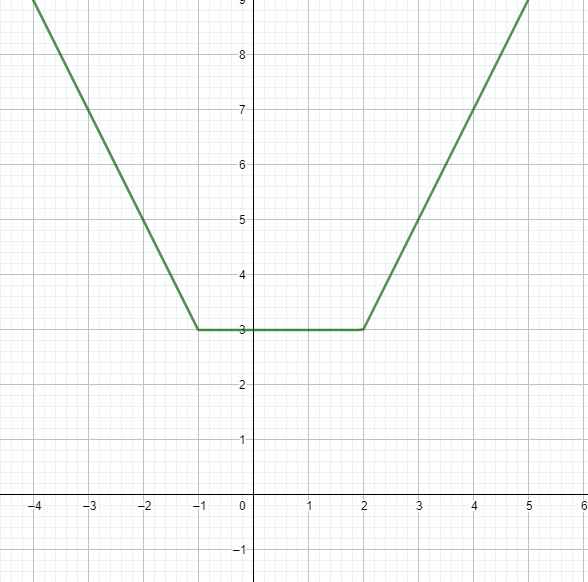
Từ đồ thị \(\Rightarrow y_{min}=3\) khi \(-1\le x\le2\)


1: Bạn bổ sung đề bài đi bạn
2: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{4}{2m-1}\\y=0\end{matrix}\right.\)
=>\(OA=\sqrt{\left(\dfrac{4}{2m-1}-0\right)^2+\left(0-0\right)^2}=\dfrac{4}{\left|2m-1\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)\cdot0-4=-4\end{matrix}\right.\)
=>OB=4
Để ΔOAB cân tại O thì OA=OB
=>\(\dfrac{4}{\left|2m-1\right|}=4\)
=>\(\dfrac{1}{\left|2m-1\right|}=1\)
=>\(\left|2m-1\right|=1\)
=>\(\left[{}\begin{matrix}2m-1=1\\2m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=2\\2m=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)

a) Hàm số đồ thị :
b) \(M(-4;m) \Rightarrow\) \(\begin{cases} x = -4\\y = m \end{cases}\)
Mà \(y = \dfrac{1}{2}x\)
\(\Rightarrow m = y = -4 . \dfrac{1}{2} = -2\)
Vậy \(m = -2 \)

a)Ta có bảng sau
| x | -1 | 0 | |||
| x+1 | - | 0 | + | / | + |
| x | - | / | - | 0 | + |
(+) với x < -1 ta có y = -x + -x - 1 = -2x - 1
(+) với -1 <= x <= 0 ta có y = -x + x + 1 = 1
(+) với x >0 ta có y = x + x + 1 = 2x + 1

b: Thay x=2 vào hàm số, ta được:
\(y=\dfrac{-1}{2}\cdot2^2=-2\)
x
xét khoảng với:+) X<0 => y=-1
+) 0=<x<=1 => y =2x-1
+) x>1 => y =1...
vẽ hàm số bình thường...sau đó chỉ lấy x thỏa mãn trên khoảng txđ
Hỏi tổng thống Brack Obama trả lời cho ?