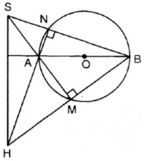
Cho đường tòn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tòn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 2 2017
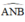là góc nội tiếp chắn nửa đường tròn ⇒ 
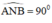⇒ AN ⊥ NB
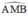là góc nội tiếp chắn nửa đường tròn ⇒ 
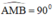⇒ AM ⊥ MB
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
Kiến thức áp dụng
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Trong một tam giác, ba đường cao đồng quy tại trực tâm.
CM
6 tháng 11 2019
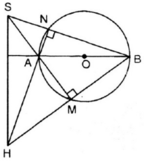
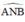là góc nội tiếp chắn nửa đường tròn ⇒ 
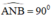⇒ AN ⊥ NB
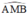là góc nội tiếp chắn nửa đường tròn ⇒ 
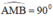⇒ AM ⊥ MB
ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.
⇒ A là trực tâm của ΔSHB.
⇒ AB ⊥ SH (đpcm)
1 tháng 3 2022
Xét (O) có
^AMB = ^ANB = 900 ( góc nt chắn nửa đường tròn )
nên AN ; BM lần lượt là đường cao
mà AN giao BN = H
=> H là trực tâm => SH là đường cao thứ 3
Vậy SH vuông AB
16 tháng 2 2022
Xét (O) có : ^ANB = ^BMA = 900 ( góc nt chắn nửa đường tròn )
hay ta có AN là đường cao, BM là đường cao
mà AN cắt BM tại H hay H là trực tâm tam giác ASB
=> SH là đường cao thứ 3 trong tam giác => SH vuông AB
BM ⊥ SA (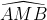
= 
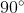vì là góc nội tiếp chắn nửa đường tròn).
Tương tự, có: AN ⊥ SB
Như vậy BM và AN là hai đường cao của tam giác SAB và H là trực tâm.
Suy ra SH ⊥ AB.
(Trong một tam giác ba đường cao đồng quy)