Cho a,b,c là số đo 3 cạnh tam giác:
Chứng minh rằng: \(1< \dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}< 2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
XO
20 tháng 1 2023
Ta có bất đẳng thức sau
a2 + b2 + c2 \(\ge\) ab + bc + ca (1)
Dấu "=" xảy ra <=> a = b = c
Thật vậy (1) <=> 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca \(\ge0\)
<=> (a - b)2 + (b - c)2 + (c - a)2 \(\ge0\) (bđt này luôn đúng)
Khi đó ta được (1) <=> 2(a2 + b2 + c2) \(\ge\) 2(ab + bc + ca)
<=> 3(a2 + b2 + c2) \(\ge\) 2ab + 2bc + 2ca + a2 + b2 + c2
<=> 3(a2 + b2 + c2) \(\ge\) (a + b + c)2
=> -(a2 + b2 + c2) \(\le\dfrac{(a+b+c)^2}{3}\)
Ta có \(P=\dfrac{b+c}{b+c-a}+\dfrac{c+a}{c+a-b}+\dfrac{a+b}{a+b-c}\)
\(=\dfrac{a}{b+c-a}+\dfrac{b}{a+c-b}+\dfrac{c}{a+b-c}+3\)
\(=\dfrac{a^2}{ab+ac-a^2}+\dfrac{b^2}{ab+bc-b^2}+\dfrac{c^2}{ac+bc-c^2}+3\)
\(\ge\dfrac{\left(a+b+c\right)^2}{ab+ac-a^2+ab+bc-b^2+ac+bc-c^2}+3\) (BĐT Schwarz)
\(=\dfrac{\left(a+b+c\right)^2}{2ab+2ac+2bc-a^2-b^2-c^2}+3\)
\(=\dfrac{\left(a+b+c\right)^2}{\left(a+b+c\right)^2-2\left(a^2+b^2+c^2\right)}+3\)
\(\ge\dfrac{\left(a+b+c\right)^2}{\left(a+b+c\right)^2-\dfrac{2}{3}\left(a+b+c\right)^2}+3=\dfrac{1}{1-\dfrac{2}{3}}+3=6\) (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2020
\(VT=\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}=\dfrac{a^2}{ab+ac}+\dfrac{b^2}{bc+ab}+\dfrac{c^2}{ac+bc}\)
\(VT\ge\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)}\ge\dfrac{3\left(ab+bc+ca\right)}{2\left(ab+bc+ca\right)}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c\)
\(\Rightarrow\) Tam giác là tam giác đều
AH
Akai Haruma
Giáo viên
31 tháng 1 2021
Lời giải:
Do $a,b,c>0$ nên:\(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=\frac{a+b+c}{a+b+c}=1(1)\)
Vì $a,b,c$ là 3 cạnh tam giác nên theo BĐT tam giác thì:
$a+b>c\Rightarrow 2(a+b)>a+b+c\Rightarrow a+b>\frac{a+b+c}{2}$
$\Rightarrow \frac{c}{a+b}< \frac{2c}{a+b+c}$. Hoàn toàn tương tự với các phân thức còn lại:
\(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}< \frac{2a+2b+2c}{a+b+c}=2(2)\)
Từ $(1);(2)$ ta có đpcm.
2 tháng 5 2017
\(\left\{{}\begin{matrix}\dfrac{a}{b+c}>\dfrac{a}{a+b+c}\\\dfrac{b}{c+a}>\dfrac{b}{a+b+c}\\\dfrac{c}{a+b}>\dfrac{c}{a+b+c}\end{matrix}\right.\Rightarrow\dfrac{a}{b+c}+\dfrac{c}{c+a}+\dfrac{c}{a+b}>\dfrac{a+b+c}{a+b+c}=1\)
\(\left\{{}\begin{matrix}\dfrac{a}{b+c}< \dfrac{2a}{a+b+c}\\\dfrac{b}{c+a}< \dfrac{2b}{a+b+c}\\\dfrac{c}{a+b}< \dfrac{2c}{a+b+c}\end{matrix}\right.\Rightarrow\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}< \dfrac{2a+2b+2c}{a+b+c}=2\)
Từ trên \(\Rightarrowđpcm\)
21 tháng 3 2017
Bài 1:a,b,c ba cạnh tam giác => a,b,c dương
\(\left\{{}\begin{matrix}a+c>b\\a+b>c\\b+c>a\end{matrix}\right.\) ta có: \(\dfrac{x}{y}< \dfrac{x+p}{y+p}\forall_{x,y,p>0\&x< y}\)
\(VT=\dfrac{a}{a+b}+\dfrac{b}{c+a}+\dfrac{c}{a+b}=\dfrac{a+c}{a+b}+\dfrac{b}{c+a}< \dfrac{a+c+c}{a+b+c}+\dfrac{b+b}{a+b+c}=\)
\(=\dfrac{a+b+c+b+c}{a+b+c}< \dfrac{\left(a+b+c\right)+\left(A+b+c\right)}{a+b+c}< \dfrac{2\left(b+a+c\right)}{a+b+c}=2=VP\)
p/s: đề sao làm vậy:
mình nghi đề phải thế này: \(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}< 2\) cách làm đơn giản hơn
A
26 tháng 1 2021
+ 
+ 
≥ 3.
Đặt b + c – a = x > 0 (1); a + c – b = y > 0 (2); a + b – c = z > 0 (3)
Cộng (1) và (2) => b + c – a + a + c – b = x + y ⇔ 2c = x + y ⇔ c =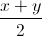 
Tương tự a =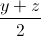 
; b =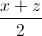 
Do đó + + = 
+ 
+ 
= 
(
+ 
+ 
+ 
+ 
+ 
)
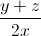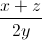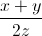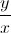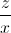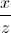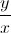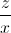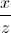= [( + ) + ( + ) + ( + )] ≥ (2 + 2 + 2) = 3.
Vậy + + ≥ 3.
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2021
Do a;b;c là 3 cạnh của 1 tam giác nên: \(\left\{{}\begin{matrix}a+b-c>0\\a+c-b>0\\b+c-a>0\end{matrix}\right.\)
BĐT đã cho tương đương:
\(\dfrac{a^2+2bc}{b^2+c^2}-1+\dfrac{b^2+2ac}{a^2+c^2}-1+\dfrac{c^2+2ab}{a^2+b^2}-1>0\)
\(\Leftrightarrow\dfrac{a^2-\left(b^2-2bc+c^2\right)}{b^2+c^2}+\dfrac{b^2-\left(a^2-2ac+c^2\right)}{a^2+c^2}+\dfrac{c^2-\left(a^2-2ab+b^2\right)}{a^2+b^2}>0\)
\(\Leftrightarrow\dfrac{a^2-\left(b-c\right)^2}{b^2+c^2}+\dfrac{b^2-\left(a-c\right)^2}{a^2+c^2}+\dfrac{c^2-\left(a-b\right)^2}{a^2+b^2}>0\)
\(\Leftrightarrow\dfrac{\left(a+c-b\right)\left(a+b-c\right)}{b^2+c^2}+\dfrac{\left(a+b-c\right)\left(b+c-a\right)}{a^2+c^2}+\dfrac{\left(b+c-a\right)\left(a+c-b\right)}{a^2+b^2}>0\) (luôn đúng)
Vậy BĐT đã cho đúng
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 2 2021
\(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(=\dfrac{b^2+c^2-a^2}{2abc}+\dfrac{a^2+c^2-b^2}{2abc}+\dfrac{a^2+b^2-c^2}{2abc}\)
\(=\dfrac{a^2+b^2+c^2}{2abc}\) (đpcm)
2 tháng 3 2021
a2 = b2 + c2 - 2bc.cosA
b2 = a2 + c2 - 2ac.cosB
c2 = a2 + b2 - 2ab.cosC
⇒ a2 + b2 + c2 = 2bc.cosA + 2ac.cosB + 2ab.cosC
⇒ VT = \(\dfrac{2bc.cosA}{2abc}+\dfrac{2ab.cosC}{2abc}+\dfrac{2ac.cosB}{2abc}\)
⇒ VT = \(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
Mình xem lại đúng là hai đề có khác tuy nhiên bản chất giống nhau kiểu như thay số khác thôi
Biểu thức cần c/m bài trước: \(B_{cu}=\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}\)
Biểu thức cần C/m bài này: \(A=\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\)
ý bạn cái mẫu không giống nhau:
Không chứng minh lại cái này nữa \(\dfrac{x}{y}< \dfrac{x+p}{x+p}\forall x,y,p>0;\left(x< y\right)\)(*) có thể quay lại câu trước xem cách chứng minh (*). ok
\(\left\{{}\begin{matrix}\dfrac{a}{b+c}< \dfrac{a+a}{a+b+c}\\\dfrac{b}{c+a}< \dfrac{b+b}{a+b+c}\\\dfrac{c}{c+a}< \dfrac{c+c}{a+b+c}\end{matrix}\right.\) công hết lai
\(VT=A< VP=\dfrac{2a+2b+2c}{a+b+c}=2\)
Bạn thấy hai bài giống nhau chưa
OK
cái này có quá nhiều rồi bạn bấm vào cái nút góc trên tay phải hình mũi tên quay xuống thấy --> tha hồ lựa chọn
đừng đăng câu khi quá nhiều.
đấy là ý kiến riêng mình thấy vậy
và khuyên các bạn giải bài gặp bài lập lại nhiều quá đừng giải nữa => nhàm chán chẳng có hứng gì