Tính tổng : P = 12 + 32 + 52+ ...... + 992
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
1
M
0
NT
0
16 tháng 9
Sửa đề: \(P=2\cdot101+3\cdot100+4\cdot99+\cdots+99\cdot4+100\cdot3+101\cdot2\)
Ta có: \(P=2\cdot101+3\cdot100+4\cdot99+\cdots+99\cdot4+100\cdot3+101\cdot2\)
\(=2\left(2\cdot101+3\cdot100+4\cdot99+\cdots+51\cdot52\right)\)
\(=2\left\lbrack2\cdot\left(103-2\right)+3\left(103-3\right)+\cdots+51\left(103-51\right)\right\rbrack\)
\(=2\cdot\left\lbrack103\left(2+3+\cdots+51\right)-\left(2^2+3^2+\cdots+51^2\right)\right\rbrack\)
\(=2\cdot\left\lbrack103\cdot\left(51-2+1\right)\cdot\frac{\left(51+2\right)}{2}-\left(1^2+2^2+\cdots+51^2\right)+1^2\right\rbrack\)
\(=2\cdot\left\lbrack103\cdot50\cdot\frac{53}{2}-\frac{51\cdot\left(51+1\right)\left(2\cdot51+1\right)}{6}+1\right\rbrack\)
\(=2\cdot\left\lbrack103\cdot25\cdot53-\frac{51\cdot52\cdot103}{6}+1\right\rbrack=2\cdot\left\lbrack103\cdot25\cdot53-17\cdot26\cdot103+1\right\rbrack\)
=181900
Ta có: \(Q=2^2+3^2+\cdots+101^2\)
\(=1^2+2^2+3^2+\cdots+101^2-1\)
\(=101\left(101+1\right)\cdot\frac{\left(2\cdot101+1\right)}{6}-1=101\cdot102\cdot\frac{203}{6}-1\)
\(=101\cdot17\cdot203-1=348551-1=348550\)
P+Q
=181900+348550
=530450
BD
19 tháng 6 2023
\(A=1^2+2^2+3^2+....+10^2\\ A=1^{ }+\left(1+1\right)\cdot2+3\cdot\left(2+1\right)+.....+10\cdot\left(9+1\right)\\ A=1+2\cdot1+2+3\cdot2+3+....+10\cdot9+10\\ A=\left(1+2+3...+10\right)+\left(1\cdot2+3\cdot2+.....+10\cdot9\right)\)
Gọi 1+2+3+...+10 là P
Số số hạng là: (10 - 1) : 1 +1 = 10 (số)
P = (10+1) . 10 : 2 = 55
P = 55
Gọi \(1\cdot2+2\cdot3+....+9\cdot10\) là C
\(C=1\cdot2+2\cdot3+....+9\cdot10\\ 3\cdot C=1\cdot2\cdot3+2\cdot3\cdot3+....+9\cdot10\cdot3\\ 3\cdot C=1\cdot2\cdot3+2\cdot3\cdot\left(4-1\right)+....+9\cdot10\cdot\left(11-8\right)\\ 3\cdot C=1\cdot2\cdot3+2\cdot3\cdot4-1\cdot2\cdot3+.....+9\cdot10\cdot11-8\cdot9\cdot10\\ 3\cdot C=9\cdot10\cdot11\\ 3\cdot C=990\\ C=330\)
\(=>A=P+C\\ =>A=55+330\\ A=385\)
b)
\(B=5^2+10^2+15^2+...+50^2\\ B=5^2+\left(2\cdot5\right)^2+\left(3\cdot5\right)^2+....+\left(5\cdot10\right)^2\\ B=5^2+2^2\cdot5^2+3^2\cdot5^2+...+5^2\cdot10^2\\ B=5^2\cdot\left(1+2^2+3^2+....+10^2\right)\\ B=25\cdot\left(1+2^2+3^2+....+10^2\right)\)
\(\left(1+2^2+3^2+....+10^2\right)=A\)
\(=>B=25\cdot A\\ B=25\cdot385\\ B=9625\)
22 tháng 10 2020
a) \(=\left(127+73\right)^2=200^2=40000\)
b) \(=18^8-\left(18^8-1\right)=1\)
c) \(=\left(100+99\right)\left(100-99\right)+\left(98+97\right)\left(98-97\right)+...+\left(2+1\right)\left(2-1\right)\)
\(=100+99+98+97+...+2+1=5050\)
d) biến đổi thành \(20^2-19^2+18^2-17^2+..+2^2-1^2\)
rồi giải ra như trên
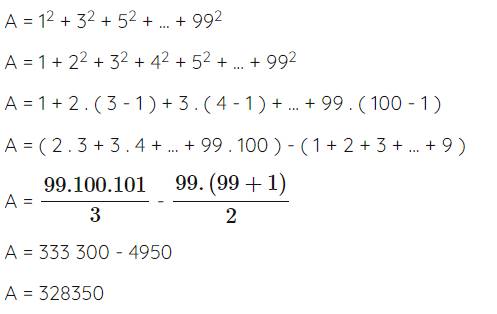
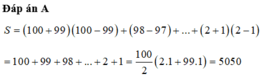
click vao cau hoi tuong tu
nếu đúng thì tick cho mình nha các bạn