Tính tổng \(S=1+0,9+\left(0,9\right)^2+\left(0,9\right)^3+....+\left(0,9\right)^{n-1}+...\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2020
\(A=lim\frac{\sqrt{n+2}+\sqrt{n+1}}{1}=lim\left[n\left(\sqrt{1+\frac{2}{n}}+\sqrt{1+\frac{1}{n}}\right)\right]=+\infty.2=+\infty\)
\(B=lim\frac{8^3.64^n-9.27^n}{4^4.64^n+5^3.25^n}=\frac{8^3-9.\left(\frac{27}{64}\right)^n}{4^4+5^3\left(\frac{25}{64}\right)^n}=\frac{8^3}{4^4}=2\)
\(1;-\frac{1}{2};\frac{1}{4}...\) là dãy cấp số nhân lùi vô hạn có \(u_1=1\) và \(q=-\frac{1}{2}\)
Do \(\left|q\right|< 1\) nên theo công thức tổng cấp số nhân:
\(S_n=\frac{u_1}{1-q}=\frac{1}{1+\frac{1}{2}}=\frac{2}{3}\)
2 tháng 2 2022
\(=\dfrac{\left(-5\right)\cdot0.81}{\left(\dfrac{5}{2}\right)^4\cdot\left(-\dfrac{10}{3}\right)^3\cdot\left(-1\right)}=\dfrac{-5\cdot0.81}{\dfrac{5^4\cdot10^3}{2^4\cdot3^3}}\)
\(=-4.05:\dfrac{5^7}{3^3\cdot2}=\dfrac{-81}{20}\cdot\dfrac{3^3\cdot2}{5^7}=\dfrac{-3^7\cdot2}{2^2\cdot5^8}=\dfrac{-3^7}{2\cdot5^8}\)
G
1
MT
12 tháng 7 2015
\(\frac{\left(0,9\right)^5}{\left(0,3\right)^6}=\frac{\left(3.0,3\right)^5}{\left(0,3\right)^6}=\frac{3^5.\left(0,3\right)^5}{\left(0,3\right)^6}=\frac{3^5}{0,3}=\frac{243}{0,3}=810\)
TH
4
TH
2 tháng 10 2021
GIÚP MÌNH VỚI MN ƠIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
2 tháng 10 2021
\(A=\dfrac{\left(20.5\right)^5.5^5}{100^5}=\dfrac{100^5.3125}{100^5}=3125\)
\(B=\dfrac{\left(0,3.3\right)^5}{\left(0,3\right)^5.0,3}=\dfrac{\left(0,3\right)^5.3^5}{\left(0,3\right)^5.0,3}=\dfrac{3^5}{0,3}=810\)
10 tháng 12 2022
a: \(=\left\{\left[\left(20-\dfrac{1}{4}\right)\cdot0.2\right]+\dfrac{3}{20}\right\}\cdot5:\left[\left(2+\dfrac{25}{11}\cdot\dfrac{22}{100}\cdot10\right)\cdot\dfrac{1}{33}\right]\)
\(=\left\{\left[\dfrac{79}{20}+\dfrac{3}{20}\right]\right\}\cdot5:\left[\dfrac{356}{55}\cdot\dfrac{1}{33}\right]\)
\(=\dfrac{82}{20}\cdot5:\dfrac{3856}{1815}\simeq104,516\)
b: \(=\dfrac{13}{30}+\dfrac{28}{45}\cdot\dfrac{5}{2}\cdot\left[\dfrac{5}{6}:\dfrac{53}{90}\right]\cdot\dfrac{53}{50}\)
\(=\dfrac{13}{30}+\dfrac{14}{9}\cdot\dfrac{3}{2}=\dfrac{83}{30}\)
18 tháng 12 2016
c) \(\frac{0,375-0,3+\frac{3}{11}+\frac{3}{12}}{0,625-0,5+\frac{5}{11}+\frac{5}{12}}=\frac{3\left(0,125-0,1+\frac{1}{11}+\frac{1}{12}\right)}{5\left(0,123-0,1+\frac{1}{11}+\frac{1}{12}\right)}=\frac{3}{5}\)
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a)\(\frac{{ - 1}}{6} + 0,75 = \frac{{ - 1}}{6} + \frac{3}{4} = \frac{{ - 2}}{{12}} + \frac{9}{{12}} = \frac{7}{{12}}\);
b)\(3\frac{1}{{10}} - \frac{3}{8} = \frac{{31}}{{10}} - \frac{3}{8} = \frac{{124}}{{40}} - \frac{{15}}{{40}} = \frac{{109}}{{40}}\);
c)
\(\begin{array}{l}0,1 + \frac{{ - 9}}{{17}} - \left( { - 0,9} \right) = \frac{1}{{10}} + \frac{{ - 9}}{{17}} + \frac{9}{{10}}\\ = (\frac{1}{{10}} + \frac{9}{{10}}) + \frac{{ - 9}}{{17}} = 1 + \frac{{ - 9}}{{17}} =\frac{{ 17}}{{17}}+\frac{{ - 9}}{{17}}= \frac{8}{{17}}\end{array}\)
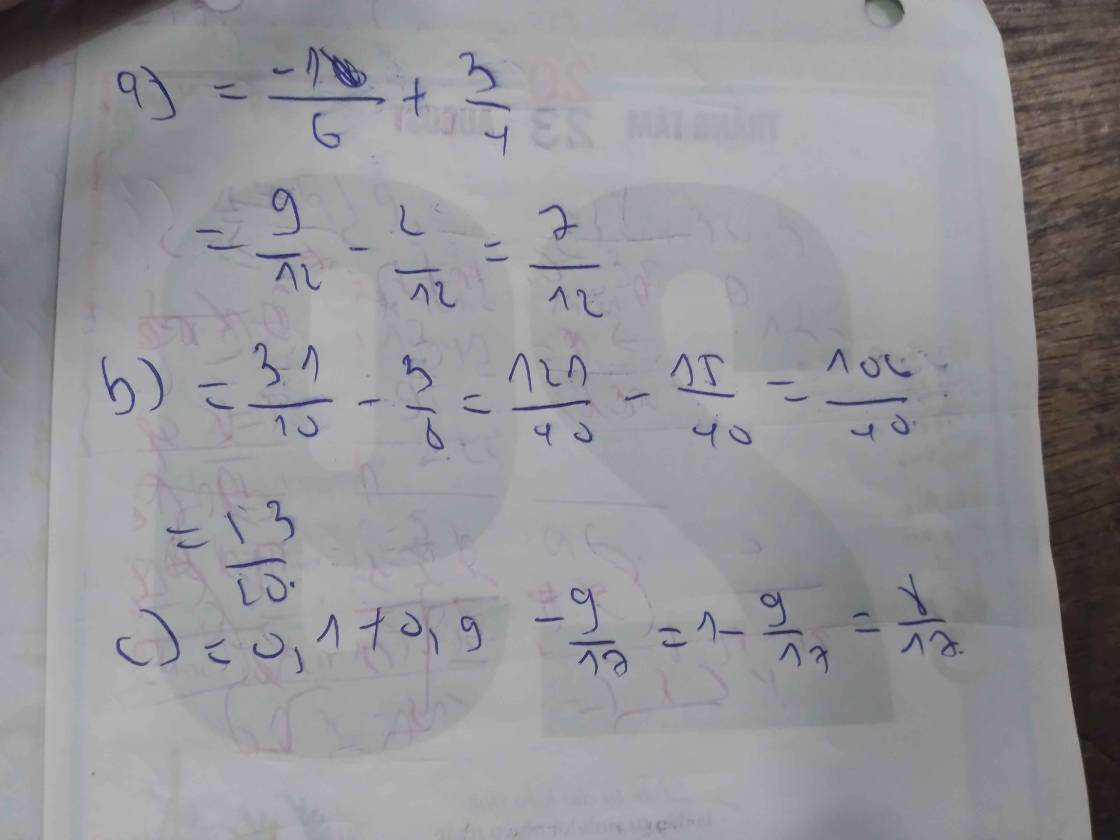
S = 1 + 0,9 + 0,9^2 + ...+ 0,9^n + ...
S là tổng của csn có u1 = 1, q = 0,9 (có |q| < 1)
S = u1 / (1 - q) = 1 / (1 - 0,9) = 10.