Tính tổng các cấp số nhân lùi vô hạn \(1;-\dfrac{1}{2};\dfrac{1}{4};-\dfrac{1}{8};.....;\left(-\dfrac{1}{2}\right)^{n-1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 6 2019
a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
CM
14 tháng 7 2017
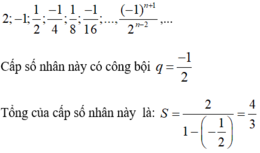
Đáp án B
- Cách giải:
Cho cấp số nhân lùi vô hạn
u
n
có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức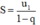 
JE
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2021
Cấp số nhân lùi vô hạn có \(u_1=1\) và \(q=\dfrac{1}{2}\)
\(\Rightarrow S=\dfrac{u_1}{1-q}=\dfrac{1}{1-\dfrac{1}{2}}=2\)
PT
1
CM
4 tháng 2 2017
+ Cấp số nhân vô hạn (un) có công bội q thỏa mãn |q| < 1 được gọi là một CSN lùi vô hạn.
+ Tổng của cấp số nhân lùi vô hạn :
13 tháng 7 2023
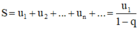
a: \(S=\dfrac{\dfrac{2}{3}}{\dfrac{5}{4}}=\dfrac{8}{15}\)
b: 1,(6)=5/3
Đáp số là 2/3