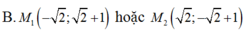Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \(\left(x-1\right)\left(^2y+2\right)^2=9\) và đường thẳng \(d:3x-4y+m=0\). Tìm m để trên d có duy nhất một điểm P mà từ đó có thể kẻ được hai tiếp tuyến PA, PB với (C) (A, B là các tiếp điểm) sao cho tam giác PAB đều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
20 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
21 tháng 7 2018
Đáp án A
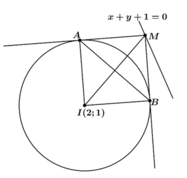
- Do M thuộc d suy ra M( t; -1-t).
Nếu 2 tiếp tuyến vuông góc với nhau thì MAIB là hình vuông
(A; B là 2 tiếp điểm).
Do đó:
- Ta có :
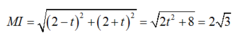
- Do đó : 2t2+ 8= 12
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1 2021
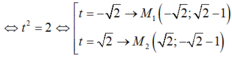
M thuộc d, quỹ tích những điểm N thỏa mãn \(2\overrightarrow{OM}+\overrightarrow{ON}=\overrightarrow{0}\) là ảnh của d qua phép vị tự tâm O tỉ số \(k=-2\)
\(\Rightarrow\) Quỹ tích N là đường thẳng d' có pt \(x+y-6=0\)
d' không cắt (C) nên không tồn tại cặp điểm M, N nào thỏa mãn yêu cầu
16 tháng 5 2022
Phương trình hoành độ giao điểm là:
\(x^2-3x-m^2+1=0\)
\(a=1;b=-3;c=-m^2+1\)
\(\text{Δ}=9-4\cdot1\cdot\left(-m^2+1\right)\)
\(=9+4m^2-4=4m^2+5>0\)
Do đó: (P) luôn cắt (d) tại hai điểm phân biệt
28 tháng 3 2023
(C): x^2+y^2+4x-2y-4=0
=>(x+2)^2+(y-1)^2=9
=>I(-2;1); R=3
M thuộc d nên M(a;1-a)
M nằm ngoài (C) nên IM>R
=>IM^2>9
=>2a^2+4a-5>0
MA^2=MB^2=IM^2-IA^2=(a+2)^2+(-a)^2-9=2a^2+4a-5
=>x^2+y^2-2ax+2(a-1)y-6a+6=0(1)
A,B thuộc (C)
=>Tọa độ A,B thỏa mãn phương trình:
x^2+y^2+4x-2y-4=0(2)
(1)-(2)=(a+2)x-ay+3a-5=0(3)
Tọa độ A,B thỏa mãn (3) nên (3) chính là phương trình đường thẳng AB
(E) tiếp xúc AB nên (E): R1=d(E,AB)
Chu vi của (E) lớn nhất khi R1 lớn nhất
=>d(E;AB) lớn nhất
Gọi H là hình chiếu vuông góc của E lên AB
=>d(E,Δ)=EH<=EK=căn 10/2
Dấu = xảy ra khi H trùng K
=>AB vuông góc EK
vecto EK=(-1/2;3/2), AB có VTCP là (a;a+2)
AB vuông góc EK
=>-1/2a+3/2(a+2)=0
=>a=-3
=>M(-3;4)
21 tháng 6 2023
I(x,y) có tung độ dương nên y>0 và thuộc (d)
nên I(x;-3x-4)
y>0
=>-3x-4>0
=>-3x>4
=>x<-4/3
Theo đề, ta có: d(I;Ox)=d(I;Oy)=R
(C) tiếp xúc với Ox,Oy nên |x|=|-3x-4|
=>3x+4=x hoặc -3x-4=x
=>2x=-4 hoặc -4x=4
=>x=-2(nhận) hoặc x=-1(loại)
=>I(-2;2)
R=|2|=2
=>(C): (x+2)^2+(y-2)^2=4
=>B
21 tháng 6 2023
I(x,y) có tung độ dương nên y>0 và thuộc (d)
nên I(x;-3x-4)
y>0
=>-3x-4>0
=>-3x>4
=>x<-4/3
Theo đề, ta có: d(I;Ox)=d(I;Oy)=R
(C) tiếp xúc với Ox,Oy nên |x|=|-3x-4|
=>3x+4=x hoặc -3x-4=x
=>2x=-4 hoặc -4x=4
=>x=-2(nhận) hoặc x=-1(loại)
=>I(-2;2)
R=|2|=2
=>(C): (x+2)^2+(y-2)^2=4
=>B
16 tháng 5 2022
Thay y=1 vào (P), ta được:
\(x^2=1\)
=>x=1 hoặc x=-1
Thay x=1 và y=1 vào (d), ta được:
\(m^2-1+3=1\)(vô lý)
Thay x=-1 và y=1 vào (d), ta được:
\(m^2-1-3=1\)
\(\Leftrightarrow m^2=5\)
hay \(m\in\left\{\sqrt{5};-\sqrt{5}\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 1 2022
Phương trình hoành độ giao điểm:
\(x^2=2\left(m-2\right)x+5\Leftrightarrow x^2-2\left(m-2\right)x-5=0\)
Do \(ac=-5< 0\Rightarrow\) phương trình luôn có 2 nghiệm trái dấu
\(\Rightarrow x_1< 0< x_2\Rightarrow x_2+2>0\)
Theo hệ thức Viet: \(x_1+x_2=2\left(m-2\right)\)
Ta có:
\(\left|x_1\right|-\left|x_2+2\right|=10\)
\(\Leftrightarrow-x_1-x_2-2=10\)
\(\Leftrightarrow-2\left(m-2\right)=12\)
\(\Leftrightarrow m=-4\)
8 tháng 7 2023
a: Thay x=-1 và y=3 vào (d), ta được:
-2-m+1=3
=>-1-m=3
=>m=-4
b: PTHĐGĐ là;
1/2x^2-2x+m-1=0
=>x^2-4x+2m-2=0
Δ=(-4)^2-4(2m-2)
=16-8m+8=-8m+24
Để (d) cắt (P) tại hai điểm phân biệt thì -8m+24>0
=>m<3
x1x2(y1+y2)+48=0
=>x1x2(x1^2+x2^2)+48=0
=>(2m-2)[4^2-2(2m-2)]+48=0
=>(2m-2)(16-4m+4)+48=0
=>(2m-2)*(20-4m)+48=0
=>40m-8m^2-40+8m+48=0
=>-8m^2+48m+8=0
=>m=3+căn 10 hoặc m=3-căn 10