giúp mình giải chi tiết với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Fe3O4 + 3H2 -> 3Fe + 4H2O
232 3\(\times\)56 (M)
\(mFe3O4=1.5\times80\%=1.2\) tấn
\(mFe=\dfrac{1.2\times3\times56}{232}=0.87\) tấn
Chọn D



a.
Công thức góc cơ bản: \(cos\left(a+k\pi\right)=\pm cosa\) ; \(sin\left(a+k2\pi\right)=sina\) ; \(cos\left(a+\dfrac{\pi}{2}\right)=-sina\)
Do đó pt tương đương:
\(2cosx+\dfrac{1}{3}cos^2x=\dfrac{8}{3}+sin2x-3sinx+\dfrac{1}{3}sin^2x\)
\(\Leftrightarrow6cosx+1-sin^2x=8+3sin2x-9sinx+sin^2x\)
\(\Leftrightarrow2sin^2x-9sinx+7+6sinx.cosx-6cosx=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sinx-7\right)+6cosx\left(sinx-1\right)=0\)
\(\Leftrightarrow\left(sinx-1\right)\left(2sinx+6cosx-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\\2sinx+6cosx=7\left(1\right)\end{matrix}\right.\)
Xét (1), ta có \(2^2+6^2=40< 7^2\) nên (1) vô nghiệm
Vậy họ nghiệm của pt là \(x=\dfrac{\pi}{2}+k2\pi\)
b.
Ta có:
\(tan^2x\left(1-sin^3x\right)+cos^3x-1=0\)
\(\Leftrightarrow\dfrac{\left(1-cos^2x\right)\left(1-sin^3x\right)}{\left(1-sin^2x\right)}-\left(1-cos^3x\right)=0\)
\(\Leftrightarrow\dfrac{\left(1-cosx\right)\left(1+cosx\right)\left(1+sinx+sin^2x\right)}{1+sinx}-\left(1-cosx\right)\left(1+cosx+cos^2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\Rightarrow x=k2\pi\\\dfrac{\left(1+cosx\right)\left(1+sinx+sin^2x\right)}{1+sinx}=1+cosx+cos^2x\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Rightarrow\left(1+cosx\right)\left(1+sinx+sin^2x\right)=\left(1+sinx\right)\left(1+cosx+cos^2x\right)\)
\(\Leftrightarrow sin^2x+sin^2x.cosx=cos^2x+cos^2x.sinx\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx+cosx\right)+sinx.cosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx-cosx=0\Rightarrow x=\dfrac{\pi}{4}+k\pi\\sinx+cosx+sinx.cosx=0\left(2\right)\end{matrix}\right.\)
Xét (2), đặt \(sinx+cosx=t\Rightarrow\left|t\right|\le\sqrt{2}\)
\(sinx.cosx=\dfrac{t^2-1}{2}\)
Pt (2) trở thành:
\(t+\dfrac{t^2-1}{2}=0\Leftrightarrow t^2+2t-1=0\Rightarrow\left[{}\begin{matrix}t=-1+\sqrt{2}\\t=-1-\sqrt{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}-1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}-1}{\sqrt{2}}\)
\(\Rightarrow...\)


câu 1 là 2 cạnh góc vuông hay 1 cạnh góc vuông và cạnh huyền thế
câu 2 AC là cạnh góc vuông hay cạnh huyền
1. Xét \(\Delta\)ABC vuông tại A, theo tỉ số lượng giác ta có
\(\cos B=\dfrac{AB}{BC}=\dfrac{6}{10}\Rightarrow B=53^O\\ C=A-B=90^o-53^o=37^o\\ AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8\)
2. Xét \(\Delta\)ABC vuông tại A, theo tỉ số lượng giác ta có
\(\sin C=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{\sin C}=\dfrac{5}{sin30}=10\\ AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-5^2}=5\sqrt{3}\\ B=A-C=90^o-30^o=60^o\)







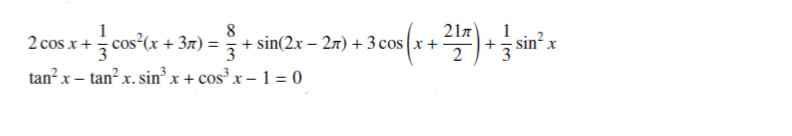

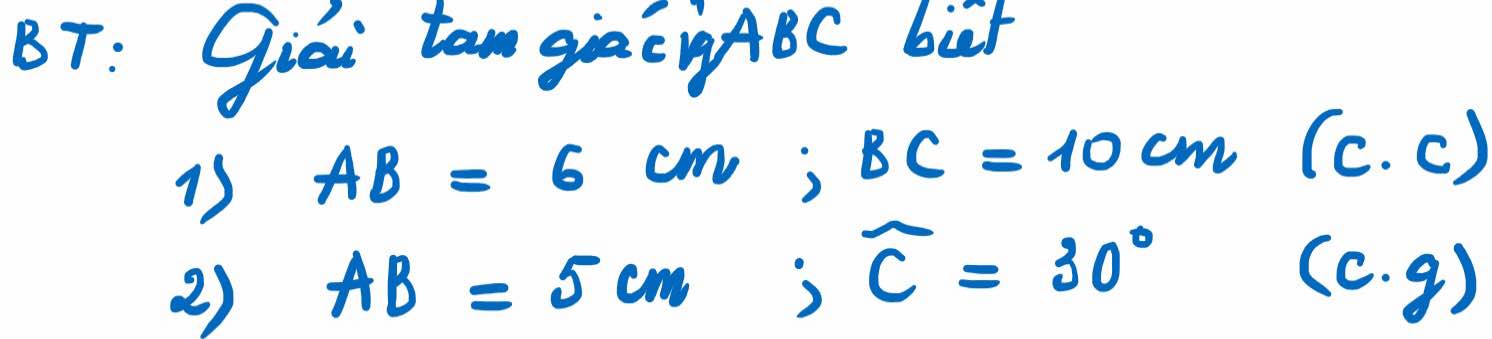
a. điều kiện : \(\hept{\begin{cases}x\ge0\\x-1\ne0\\x\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x>0\\x\ne1\end{cases}}}\)
b, ta có : \(A=\left(\frac{\sqrt{x}-2}{\left(x+2\sqrt{x}+1\right)}-\frac{\sqrt{x}+2}{x-1}\right)\times\frac{x-1}{2\sqrt{x}}\)
\(=\left(\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right)\times\frac{x-1}{2\sqrt{x}}\)
\(=-\frac{6\sqrt{x}}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\times\frac{x-1}{2\sqrt{x}}=\frac{3}{\sqrt{x}+1}\)
c. Để A nguyên thì \(\sqrt{x}+1\) là ước của 3 hay : \(\orbr{\begin{cases}\sqrt{x}+1=1\\\sqrt{x}+1=3\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\left(\text{ loại}\right)\\x=4\end{cases}}}\)