Chứng minh rằng số đường chéo của một đa giác lồi n cạnh là : \(\dfrac{n\left(n-3\right)}{2}\) ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
18 tháng 12 2019
Đa giác lồi n cạnh có n đỉnh.
Chọn 2 điểm bất kì trong số các đỉnh của một đa giác ta được 1 cạnh hoặc 1 đường chéo của đa giác.
⇒Tổng số cạnh và đường chéo của đa giác bằng:
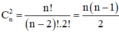
⇒ số đường chéo của đa giác lồi có n cạnh là:
KQ
10 tháng 2 2016
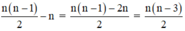
Ta chứng minh khẳng định đúng với mọi n ε N* , n ≥ 4.
Với n = 4, ta có tứ giác nên nó có hai đường chéo.
Mặt khác thay n = 4 vào công thức, ta có số đường chéo của tứ giác theo công thức là: = 2
Vậy khẳng định là đúng với n= 4.
Giả sử khẳng định là đúng với n = k ≥ 4, tức là đa giác lồi k cạnh có
số đường chéo là
Ta phải chứng minh khẳng định đúng với n = k + 1. Nghĩa là phải chứng minh đa giác lồi k + 1cạnh có số đường chéo là
Xét đa giác lồi k + 1 cạnh
Nối A1 và Ak, ta được đa giác k cạnh A1A2…Ak có đường chéo (giả thiết quy nạp). Nối Ak+1 với các đỉnh A2, A3, …, Ak-1, ta được thêm k -2 đường chéo, ngoài ra A1Ak cũng là một đường chéo.
Vậy số đường chéo của đa giác k + 1 cạnh là
+ k - 2 + 1 =
Như vậy, khẳng định cũng đúng với đa giác k + 1 cạnh
KQ
10 tháng 2 2016
Ta chứng minh khẳng định đúng với mọi n ε N* , n ≥ 4.
Với n = 4, ta có tứ giác nên nó có hai đường chéo.
Mặt khác thay n = 4 vào công thức, ta có số đường chéo của tứ giác theo công thức là: = 2
Vậy khẳng định là đúng với n= 4.
Giả sử khẳng định là đúng với n = k ≥ 4, tức là đa giác lồi k cạnh có
số đường chéo là
Ta phải chứng minh khẳng định đúng với n = k + 1. Nghĩa là phải chứng minh đa giác lồi k + 1cạnh có số đường chéo là
Xét đa giác lồi k + 1 cạnh
Nối A1 và Ak, ta được đa giác k cạnh A1A2…Ak có đường chéo (giả thiết quy nạp). Nối Ak+1 với các đỉnh A2, A3, …, Ak-1, ta được thêm k -2 đường chéo, ngoài ra A1Ak cũng là một đường chéo.
Vậy số đường chéo của đa giác k + 1 cạnh là
+ k - 2 + 1 =
Như vậy, khẳng định cũng đúng với đa giác k + 1 cạnh
duyệt lẹ
19 tháng 3 2020
Đặt n(n-3)/2 (*)
*)Với n=4 => có 4(4-3)/2=2
=> * đúng với n =2
*)Giả sử (*)đúng với n=k có => k(k-3)/2 với đa giác lồi có k cạnh
*) Ta chứng minh cho (*) đúng với n=k+1 <=> đa giác lồi k+1 cạnh có (k+1)(k-2)/2 đường chéo.
Thật vậy,để ý rằng,đa giác lồi có k cạnh nếu thêm 1 đỉnh sẽ có thêm k-1 đường chéo
=>
số đường chéo của đa giác lồi k+1 cạnh là :
k(k-3)/2 +k-1= (k^2-k-2)/2=(k+1)(k-2)/2 (đúng)
=> đpcm
25 tháng 2 2017
Giải
a) Vẽ một n - giác lồi rồi vẽ các đường chéo xuất phát từ một đỉnh của n - giác lồi đó, ta được (n - 2) tam giác
Tổng các góc của hình n - giác lồi bằng tổng các góc của (n - 2) tam giác, tức là có số đo bằng (n - 2).1800
Hình n - giác đều có n góc bằng nhau nên mỗi góc có số đo là \(\frac{\left(n-2\right).180^{0^{ }}}{n}\)
b) Với hình lục giác đều ta có n = 6, nên số đo góc của nó là\(\frac{\left(6-2\right).180^0}{6}=120^0\)
Với hình bát giác đều ta có n = 8, nên số đo góc của nó là \(\frac{\left(8-2\right).180^0}{8}=135^0\)
21 tháng 7 2019
hình n giác vẽ các đường chéo từ 1 đỉnh bất kỳ của đa giác đó
khi đó các đuờng chéo và các cạnh tạo thành (n-2) tam giác
nên ta được tổng số đo các góc của n giác chính là tổng số đo của ( n -2) tam giác
suy ra : tổng số đo các góc là : ( n- 2) . 180
học tốt
LN
4 tháng 6 2015
theo bạn nói thì đa giác lồi có n(n-3) :2 đường chéo
Mà đa giác lồi này có 170 đường chéo
=> n(n-3):2 = 170
=> n(n-3) = 340
=> n(n-3) = 20.17
<=> n = 20
Vậy đa giác lồi này có 20 cạnh
Ta chứng minh khẳng định đúng với mọi n ε N* , n ≥ 4.
Với n = 4, ta có tứ giác nên nó có hai đường chéo.
Mặt khác thay n = 4 vào công thức, ta có số đường chéo của tứ giác theo công thức là: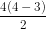
= 2
Vậy khẳng định là đúng với n= 4.
Giả sử khẳng định là đúng với n = k ≥ 4, tức là đa giác lồi k cạnh có
số đường chéo là
Ta phải chứng minh khẳng định đúng với n = k + 1. Nghĩa là phải chứng minh đa giác lồi k + 1cạnh có số đường chéo làVậy số đường chéo của đa giác k + 1 cạnh là
Như vậy, khẳng định cũng đúng với đa giác k + 1 cạnh