Chứng tỏ rằng với mọi số phức \(z\), ta luôn có phần thực và phần ảo của \(z\) không vượt qua môđun của nó ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
PT
1

CM
6 tháng 11 2018
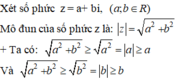
Vậy với mọi số phức thì phần thực và phần ảo của nó không vượt quá mô đun của nó.
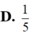

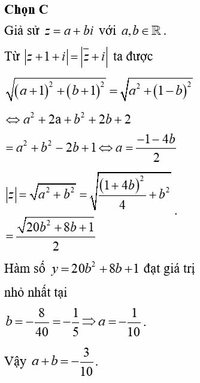
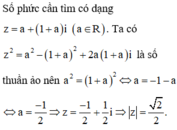


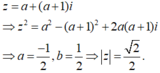
Giả sử z = a + bi
Khi đó: |z|=√a2+b2|z|=a2+b2
Từ đó suy ra:
|z|=√a2=|a|≥a,|z|=√b2=|b|≥b