Tính:
a. \(\sqrt{\dfrac{289}{225}};\) b. \(\sqrt{2\dfrac{14}{25}};\) c. \(\sqrt{\dfrac{0,25}{9}};\) d. \(\sqrt{\dfrac{8,1}{1,6}}.\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 11 2017
Ta có :
\(\sqrt{225}-\left(\dfrac{1}{\sqrt{13}}-1\right)=15-\dfrac{1}{\sqrt{13}}+1=16-\dfrac{1}{\sqrt{13}}\)
\(\sqrt{289}-\left(\dfrac{1}{\sqrt{14}}+1\right)=17-\dfrac{1}{\sqrt{14}}-1=16-\dfrac{1}{\sqrt{14}}\)
Vì 13 < 14 \(\Rightarrow\sqrt{13}< \sqrt{14}\)
\(\Rightarrow\dfrac{1}{\sqrt{13}}>\dfrac{1}{\sqrt{14}}\)
\(\Rightarrow16-\dfrac{1}{\sqrt{13}}< 16-\dfrac{1}{\sqrt{14}}\)
\(\Rightarrow\sqrt{225}-\left(\dfrac{1}{\sqrt{13}}-1\right)< \sqrt{289}-\left(\dfrac{1}{\sqrt{14}}+1\right)\)
3 tháng 11 2017
Ta có: \(\sqrt{225}-\left(\dfrac{1}{\sqrt{13}}-1\right)\)
\(=15-\dfrac{1}{\sqrt{13}}+1\)
\(=\left(15+1\right)-\dfrac{1}{\sqrt{13}}\)
\(=16-\dfrac{1}{\sqrt{13}}\)
Và: \(\sqrt{289}-\left(\dfrac{1}{\sqrt{14}}+1\right)\)
\(=17-\dfrac{1}{\sqrt{14}}-1\)
\(=\left(17-1\right)-\dfrac{1}{\sqrt{14}}\)
\(=16-\dfrac{1}{\sqrt{14}}\)
Vì \(13< 14\Rightarrow\sqrt{13}< \sqrt{14}\Rightarrow\dfrac{1}{\sqrt{13}}>\dfrac{1}{\sqrt{14}}\Rightarrow-\dfrac{1}{\sqrt{13}}< -\dfrac{1}{\sqrt{14}}\Rightarrow16-\dfrac{1}{\sqrt{13}}< 16-\dfrac{1}{\sqrt{14}}\)
Hay \(\sqrt{225}-\left(\dfrac{1}{\sqrt{13}}-1\right)< \sqrt{289}-\left(\dfrac{1}{\sqrt{14}}+1\right)\)
Chúc bn học tốt 
DH
21 tháng 6 2017
a, \(\sqrt{\dfrac{289}{225}}=\sqrt{\dfrac{17^2}{15^2}}=\dfrac{17}{15}\)
b, \(\sqrt{2\dfrac{14}{25}}=\sqrt{\dfrac{64}{25}}=\sqrt{\dfrac{8^2}{5^2}}=\dfrac{8}{5}\)
c, \(\sqrt{\dfrac{0,25}{9}}=\sqrt{\dfrac{0,5^2}{3^2}}=\dfrac{0,5}{3}\)
d, \(\sqrt{\dfrac{8,1}{1,6}}=\sqrt{\dfrac{0,1}{0,1}.\dfrac{81}{16}}=\sqrt{1.\dfrac{81}{16}}=\dfrac{9}{4}\)
Chúc bạn học tốt!!!
Q
21 tháng 6 2017
a) \(\sqrt{\dfrac{289}{225}}\)
\(=\dfrac{\sqrt{289}}{\sqrt{225}}\)
\(=\dfrac{\sqrt{17^2}}{\sqrt{15^2}}\)
\(=\dfrac{17}{15}\)
b) \(\sqrt{2\dfrac{14}{15}}\)
\(=\sqrt{\dfrac{44}{15}}\)
\(=\dfrac{\sqrt{44}}{\sqrt{15}}\)
\(=\dfrac{2\sqrt{11}}{\sqrt{15}}\)
\(=\dfrac{2\sqrt{165}}{15}\)
c) \(\sqrt{\dfrac{0,25}{9}}\)
\(=\sqrt{\dfrac{1}{\dfrac{4}{9}}}\)
\(=\dfrac{\dfrac{1}{2}}{3}\)
\(=\dfrac{1}{6}\)
d) \(\sqrt{\dfrac{8,1}{1,6}}\)
\(=\sqrt{5,0625}\)
\(=\sqrt{\dfrac{81}{16}}\)
\(=\dfrac{9}{4}\)
NN
12 tháng 7 2017
Giải:
Ta có tính chất tổng quát:
\(\frac{1}{\left(k+1\right)\sqrt{k}+k\left(\sqrt{k+1}\right)}=\frac{\left(k+1\right)\sqrt{k}-k\left(\sqrt{k+1}\right)}{\left(k+1\right)^2k-k^2\left(k+1\right)}\)
\(=\frac{\left(k+1\right)\sqrt{k}-k\left(\sqrt{k+1}\right)}{\left(k+1\right)k\left(k+1-k\right)}=\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}}\)
Áp dụng vào biểu thức
\(\Rightarrow A=\frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{224}}-\frac{1}{\sqrt{225}}\)
\(=1-\frac{1}{\sqrt{225}}\)
3 tháng 8 2021
a) Ta có: \(-\dfrac{3}{2}\sqrt{9-4\sqrt{5}}+\sqrt{\left(-4\right)^2\cdot\left(1+\sqrt{5}\right)^2}\)
\(=\dfrac{-3}{2}\left(\sqrt{5}-2\right)+4\cdot\left(\sqrt{5}+1\right)\)
\(=\dfrac{-3}{2}\sqrt{5}+3+4\sqrt{5}+4\)
\(=\dfrac{5}{2}\sqrt{5}+7\)
b) Ta có: \(\left(1+\dfrac{1}{\tan^225^0}\right)\cdot\sin^225^0-\tan55^0\cdot\tan35^0\)
\(=\dfrac{\tan^225^0+1}{\tan^225^0}\cdot\sin25^0-1\)
\(=\left(\dfrac{\sin^225^0}{\cos^225^0}+1\right)\cdot\dfrac{\cos^225^0}{\sin^225^0}\cdot\sin25^0-1\)
\(=\dfrac{\sin^225^0+\cos^225^0}{\cos^225^0}\cdot\dfrac{\cos^225^0}{\sin25^0}-1\)
\(=\dfrac{1}{\sin25^0}-1\)
\(=\dfrac{1-\sin25^0}{\sin25^0}\)
19 tháng 4 2021
a, \(\sqrt{\frac{289}{25}}=\frac{\sqrt{289}}{\sqrt{25}}=\frac{17}{5}\)
b, \(\sqrt{2\frac{14}{25}}=\sqrt{\frac{64}{25}}=\frac{8}{5}\)
c, \(\sqrt{\frac{0,25}{9}}=\frac{\sqrt{0,25}}{\sqrt{9}}=\frac{0,5}{3}=\frac{1}{2}.\frac{1}{3}=\frac{1}{6}\)
d, \(\sqrt{\frac{8,1}{16}}\)đề có sai ko cô ?
DC
13 tháng 5 2021
a) căn 289 / 225 = 17/15
b) căn 64/ 25 = 8/5
c) căn 0,25 / 9 = 1/6
d) căn 8,1 / 1,6 = 9/4
17 tháng 6 2018
a) \(\sqrt{\dfrac{59}{25}+\dfrac{6}{5}\sqrt{2}}=\sqrt{2+2.\dfrac{3}{5}\sqrt{2}+\dfrac{9}{25}}=\sqrt{\left(\sqrt{2}+\dfrac{3}{5}\right)^2}\)
= / \(\sqrt{2}+\dfrac{3}{5}\) / = \(\sqrt{2}+\dfrac{3}{5}\)
b) \(\sqrt{\dfrac{129}{16}+\sqrt{2}}=\sqrt{8+2.2\sqrt{2}.\dfrac{1}{4}+\dfrac{1}{16}}\)
= \(\sqrt{\left(2\sqrt{2}+\dfrac{1}{4}\right)^2}\) = / \(2\sqrt{2}+\dfrac{1}{4}\) / = \(2\sqrt{2}+\dfrac{1}{4}\)
c) Tương tự , mình bận rồi , nếu chưa biết tẹo mk làm cho.
17 tháng 6 2018
c) \(\sqrt{\dfrac{289+4\sqrt{72}}{16}}=\sqrt{\dfrac{289}{16}+\dfrac{1}{4}\sqrt{72}}=\sqrt{\dfrac{289}{16}+\dfrac{1}{4}.6\sqrt{2}}=\sqrt{18+2.\dfrac{1}{4}.3\sqrt{2}+\dfrac{1}{16}}=\sqrt{\left(3\sqrt{2}+\dfrac{1}{4}\right)^2}\) = / \(3\sqrt{2}+\dfrac{1}{4}\) / = \(3\sqrt{2}+\dfrac{1}{4}\)
a)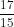
; b) 
;
c)
; d) 
.
a) \(\sqrt{\dfrac{289}{225}}=\dfrac{\sqrt{289}}{\sqrt{225}}=\dfrac{17}{15}\)
b) \(\sqrt{2\dfrac{14}{25}}=\dfrac{\sqrt{64}}{\sqrt{25}}=\dfrac{8}{5}\)
c) \(\sqrt{\dfrac{0,25}{9}}=\dfrac{\sqrt{0,25}}{\sqrt{9}}=\dfrac{0,5}{3}=\dfrac{1}{6}\)
d) \(\sqrt{\dfrac{8,1}{1,6}}=\dfrac{\sqrt{81}}{\sqrt{16}}=\dfrac{9}{4}\)