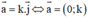Trong mặt phẳng tọa độ Oxy cho hình bình hành OABC, C nằm trên Ox. Khẳng định nào sau đây đúng ?
a) \(\overrightarrow{AB}\) có tung độ khác 0
b) A và B có tung độ khác nhau
c) C có hoành độ bằng 0
d) \(x_A+x_C-x_B=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
D
Doraemon
30 tháng 3 2017
Đúng(0)
Những câu hỏi liên quan
CM
5 tháng 6 2017
a) Đúng. Giả sử A(a; b); O(0; 0)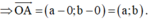 
b) Đúng
c) Đúng
d) Đúng Vì tia phân giác của góc phần tư thứ nhất là đường thẳng y = x.
CM
28 tháng 2 2018
a) Sai
Sửa lại: Điểm A nằm trên trục hoành thì có tung độ bằng 0.
b) Sai
Ví dụ: A(2; 6), B(–4; 0) có trung bình cộng các hoành độ bằng –1.
P(–1; 3) là trung điểm của AB
P(–1; 2) không phải trung điểm của AB
P(–1; 0) không phải trung điểm của AB.
c) Đúng
ABCD là hình bình hành nên giao điểm O của AC và BD đồng thời là trung điểm của AC và BD
O là trung điểm của AC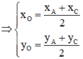 
O là trung điểm của BD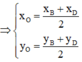 
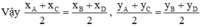
CM
20 tháng 4 2019
a) Đúng.
Hai vec tơ đối nhau thì chúng có hoành độ đối nhau và tung độ đối nhau.
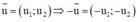
b) Sai.
Sửa lại: Vec tơ a→ cùng phương với vec tơ i→ nếu a→ có tung độ bằng 0.
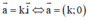
c) Đúng.
