Có 2 rổ quýt chứa số quýt bằng nhau. Nếu lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở rổ thứ 2 bằng \(\dfrac{1}{3}\) của bình phương số quả còn lại ở rổ thứ nhất. Hỏi số quả quýt ở mỗi rổ lúc ban đầu là bao nhiêu ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 5 2019
Gọi số quýt ban đầu ở mỗi rổ là x (quả)
Muốn lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở mỗi rổ lúc đầu phải nhiều hơn 30 quả hay x > 30.
Khi đó rổ thứ nhất còn x – 30 quả; rổ thứ hai có x + 30 quả.
Vì số quả ở rổ thứ hai bằng 1/3 bình phương số quả còn lại ở rổ thứ nhất nên ta có phương trình:
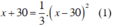
Giải phương trình (1):
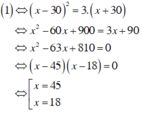
Vì x > 30 nên x = 45 thỏa mãn.
Vậy ban đầu mỗi rổ có 45 quả cam.
VV
14 tháng 5 2016
Pt cần lập là:
X+30 = 1/3(x-30)^2
Giải ta đk: x1=45(tm)
x2=18(ktm)
HM
18 tháng 11 2023
mỗi thúng hơn mỗi rổ số quả là
12 trừ 2 bằng 10 [ do bàn phím mình bị lỗi nên ko ấn được ]
số cam trong rổ là
10 chia [ 3 trừ 1] nhân 1 bằng A
còn lại bạn tự tính đi
25 tháng 7 2017
Số quýt hơn số cam là: 12 x 2 - 2 x 5 = 14(quả)
Coi số cam trong mỗi rổ là 1 phân thì số quýt trong mỗi thúng là 3 phần . Do đó tổng số cam trong 5 rổ là 5 phần và số quýt trong 2 thúng là 6 phần như thế
Tổng số cam là 14 : (6 -5) x 5 = 70 (quả)
Tổng số quýt là 70 + 14 = 84 ( quả )
28 tháng 5 2021
Gọi số cam của mỗi rổ lúc đầu là a (a > 6; a \(\in\mathbb{N}\))
Ta có \((a-6)^2=a+6\Leftrightarrow a^2-13a+30=0\Leftrightarrow (a-2)(a-10)=0\Leftrightarrow a=10\) (Do a > 6)
AT
28 tháng 5 2021
Gọi số quả cam của rổ 1 và 2 lần lượt là a,b(quả) \(\left(a,b>6\right)\)
Theo đề: \(\left\{{}\begin{matrix}a=b\\b+6=\left(a-6\right)^2\end{matrix}\right.\)
\(\Rightarrow a+6=\left(a-6\right)^2\Leftrightarrow a^2-13a+30=0\Leftrightarrow\left(a-3\right)\left(a-10\right)=0\)
mà \(a>6\Rightarrow a=10\Rightarrow a=b=10\) \(\)
Gọi x là số quýt chứa trong một rổ lúc đầu. Điều kiện x nguyên, x > 30. Ta có phương trình
⇔ x = 45 (nhận), x = 18 (loại).
Trả lời: Số quýt ở mỗi rổ lúc đầu: 45 quả.