4x2 - 12x + 5 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: \(4x\left(x-7\right)-4x^2=56\)
\(\Leftrightarrow4x^2-7x-4x^2=56\)
hay x=-8
b: Ta có: \(12x\left(3x-2\right)-\left(4-6x\right)=0\)
\(\Leftrightarrow36x^2-24x-4+6x=0\)
\(\Leftrightarrow36x^2-18x-4=0\)
\(\text{Δ}=\left(-18\right)^2-4\cdot36\cdot\left(-4\right)=900\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{18-30}{72}=\dfrac{-1}{6}\\x_2=\dfrac{18+30}{72}=\dfrac{2}{3}\end{matrix}\right.\)
c: Ta có: \(4\left(x-5\right)-\left(x-5\right)^2=0\)
\(\Leftrightarrow\left(x-5\right)\left(4-x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=9\end{matrix}\right.\)

Vì: 4 x 2 − 12 x + 11 = 4 x − 3 2 2 + 2 > 0 , ∀ x nên phương trình xác định với mọi x
Đặt 4 x 2 − 12 x + 11 = t ( t ≥ 2 )
⇔ 4 x 2 − 12 x + 1 = t 2 ⇔ 4 x 2 − 12 x + 15 = t 2 + 4
Khi đó, phương trình trở thành: t 2 − 5 t + 4 = 0 ⇔ t = 1 ( k t m ) t = 4 ( k t m )
Với t = 4 ⇔ 4 x 2 − 12 x + 11 = 16 ⇔ 4 x 2 − 12 x − 5 = 0
Tổng 2 nghiệm của phương trình là: 3
Đáp án cần chọn là: B

c: \(\Leftrightarrow\left(x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)


a) \(4x^2+12x+1=\left(4x^2+12x+9\right)-8=\left(2x+3\right)^2-8\ge-8\)
\(ĐTXR\Leftrightarrow x=-\dfrac{3}{2}\)
b) \(4x^2-3x+10=\left(4x^2-3x+\dfrac{9}{16}\right)+\dfrac{151}{16}=\left(2x-\dfrac{3}{4}\right)^2+\dfrac{151}{16}\ge\dfrac{151}{16}\)
\(ĐTXR\Leftrightarrow x=\dfrac{3}{8}\)
c) \(2x^2+5x+10=\left(2x^2+5x+\dfrac{25}{8}\right)+\dfrac{55}{8}=\left(\sqrt{2}x+\dfrac{5\sqrt{2}}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\)
\(ĐTXR\Leftrightarrow x=-\dfrac{5}{4}\)
d) \(x-x^2+2=-\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{9}{4}=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}\le\dfrac{9}{4}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{2}\)
e) \(2x-2x^2=-2\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{2}=-2\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{2}\le\dfrac{1}{2}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{2}\)
f) \(4x^2+2y^2+4xy+4y+5=\left(4x^2+4xy+y^2\right)+\left(y^2+4y+4\right)+1=\left(2x+y\right)^2+\left(y+2\right)^2+1\ge1\)
\(ĐTXR\Leftrightarrow\) \(\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
a: Ta có: \(4x^2+12x+1\)
\(=4x^2+12x+9-8\)
\(=\left(2x+3\right)^2-8\ge-8\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{3}{2}\)
b: Ta có: \(4x^2-3x+10\)
\(=4\left(x^2-\dfrac{3}{4}x+\dfrac{5}{2}\right)\)
\(=4\left(x^2-2\cdot x\cdot\dfrac{3}{8}+\dfrac{9}{64}+\dfrac{151}{64}\right)\)
\(=4\left(x-\dfrac{3}{8}\right)^2+\dfrac{151}{16}\ge\dfrac{151}{16}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{8}\)
c: Ta có: \(2x^2+5x+10\)
\(=2\left(x^2+\dfrac{5}{2}x+5\right)\)
\(=2\left(x^2+2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}+\dfrac{55}{16}\right)\)
\(=2\left(x+\dfrac{5}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{5}{4}\)

a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: 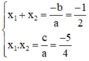
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: 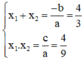
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: 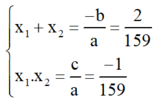

1.\(\left(x+2\right)\left(2x-3\right)=x^2-4\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3\right)-\left(x+2\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3-x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
2.\(x^2+3x+2=0\)
\(\Leftrightarrow x^2+x+2x+2=0\)
\(\Leftrightarrow x\left(x+1\right)+2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-2\end{matrix}\right.\)
3.\(2x^2+5x+3=0\)
\(\Leftrightarrow2x^2+2x+3x+3=0\)
\(\Leftrightarrow2x\left(x+1\right)+3\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
4.\(x^3+x^2-12x=0\)
\(\Leftrightarrow x\left(x^2+x-12\right)=0\)
\(\Leftrightarrow x\left(x+4\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\\x=3\end{matrix}\right.\)
a: \(\Leftrightarrow\left(x+2\right)\left(2x-3\right)-\left(x+2\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3-x+2\right)=0\)
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
b: =>(x+1)(x+2)=0
=>x=-1 hoặc x=-2
c: =>(2x+3)(x+1)=0
=>x=-1 hoặc x=-3/2
d: =>x(x+4)(x-3)=0
hay \(x\in\left\{0;-4;3\right\}\)

Để tìm cặp số (x, y) thỏa mãn phương trình 4x^2 - 12xy + 2y^2 + 12x - 6y + 8 = 0 sao cho y nhỏ nhất, ta cần tìm giá trị nhỏ nhất của y trong phương trình này.
Để làm điều này, ta có thể sử dụng phương pháp hoàn thiện định thức. Trước tiên, ta nhân hai vế của phương trình với 2 để thu được phương trình tương đương:
8x^2 - 24xy + 4y^2 + 24x - 12y + 16 = 0
Tiếp theo, ta nhóm các thành phần chứa x^2, xy và y^2 lại với nhau:
(8x^2 - 24xy + 4y^2) + (24x - 12y) + 16 = 0
(2x - y)^2 + 2(6x - 3y) + 16 = 0
Bây giờ, ta để ý rằng (2x - y)^2 là một số không âm vì là bình phương của một số. Do đó, để giá trị của phương trình là nhỏ nhất, ta cần tìm giá trị nhỏ nhất của 2(6x - 3y). Điều này xảy ra khi 6x - 3y = 0, tức là 2x - y = 0.
Giải hệ phương trình này, ta có:
2x - y = 0 6x - 3y = 0
Từ phương trình thứ nhất, ta có y = 2x. Thay vào phương trình thứ hai, ta có:
6x - 3(2x) = 0 6x - 6x = 0 0 = 0
Phương trình này đúng với mọi giá trị của x và y. Do đó, không có giá trị cụ thể cho (x, y) thỏa mãn y nhỏ nhất trong phương trình ban đầu.
\(4x^2-12x+5=0\Leftrightarrow4x^2-10x-2x+5=0\Leftrightarrow2x\left(2x-5\right)-\left(2x-5\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(2x-1\right)=0\)\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\2x-1=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy ...
4x2 - 12x + 5 = 0 <=> 4x2 - 2x - 10x + 5 =0
<=> 2x ( 2x - 1) - 5 (2x - 1) = 0
<=> (2x-5)(2x-1) = 0
=> \(\left\{{}\begin{matrix}2x-5=0< =>x=2,5\\2x-1=0< =>x=0,5\end{matrix}\right.\)
Vậy với x = 0,5 hoặc x = 2,5 thì ta đc PT trên.