tìm x biết |x2+|6x-2||=x2+4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
28 tháng 5 2022
Câu 1:
a) 2x(3x+2) - 3x(2x+3) = 6x^2+4x - 6x^2-9x = -5x
b) \(\left(x+2\right)^3+\left(x-3\right)^2-x^2\left(x+5\right)\)
\(=x^3+6x^2+12x+8+x^2-6x+9-x^3-5x^2\)
\(=2x^2+6x+17\)
c) \(\left(3x^3-4x^2+6x\right)\div\left(3x\right)=x^2-\dfrac{4}{3}x+2\)
TN
1
AH
Akai Haruma
Giáo viên
17 tháng 4 2023
Lời giải:
a.
PT $\Leftrightarrow 3x^2+\frac{x}{2}-3x^2+3x+2=0$
$\Leftrightarrow \frac{7}{2}x+2=0$
$\Leftrightarrow \frac{7}{2}x=-2$
$\Leftrightarrow x=-2: \frac{7}{2}=\frac{-4}{7}$
b.
PT $\Leftrightarrow 5x^2-3-5x^2-6x=0$
$\Leftrightarrow -3-6x=0$
$\Leftrightarrow 6x=-3$
$\Leftrightarrow x=\frac{-3}{6}=\frac{-1}{2}$
CM
18 tháng 11 2019
Đặt x2 = a (a ≥ 0), y2 = b (b ≥ 0)
Ta có: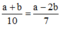 
và a2b2 = 81.
Theo tính chất của dãy tỉ số bằng nhau ta có:
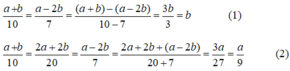
Từ (1) và (2) suy ra a/9 = b ⇒ a = 9b
Do a2b2 = 81 nên (9b)2.b2 = 81 ⇒ 81b4 = 81 ⇒ b4 = 1 ⇒ b = 1 (vì b ≥ 0)
Suy ra a = 9. 1 = 9
Ta có x2 = 9 và y2 = 1. Suy ra x = 3 hoặc x = -3, y = 1 hoặc y = -1.
TT
12 tháng 12 2020
Bạn chú ý đăng lẻ câu hỏi! 1/
a/ \(=x^3-2x^5\)
b/\(=5x^2+5-x^3-x\)
c/ \(=x^3+3x^2-4x-2x^2-6x+8=x^3=x^2-10x+8\)
d/ \(=x^2-x^3+4x-2x+2x^2-8=3x^2-x^3+2x-8\)
e/ \(=x^4-x^2+2x^3-2x\)
f/ \(=\left(6x^2+x-2\right)\left(3-x\right)=17x^2+5x-6-6x^3\)
24 tháng 9 2023
`#3107`
`a)`
`(6x - 2)^2 + 4(3x - 1)(2 + y) + (y + 2)^2 - (6x + y)^2`
`= [(6x - 2)^2 - (6x + y)^2] + 4(3x - 1)(2 + y) + (2 + y)^2`
`= (6x - 2 - 6x - y)(6x -2 + 6x + y) + (2 + y)*[ 4(3x - 1) + 2 + y]`
`= (2 - y)(12x + y - 2) + (2 + y)*(12x - 4 + 2 + y)`
`= (2 - y)(12x + y - 2) + (2 + y)*(12x + y - 2)`
`= (12x + y - 2)(2 - y + 2 + y)`
`= (12x + y - 2)*4`
`= 48x + 4y - 8`
`b)`
\(5(2x-1)^2+2(x-1)(x+3)-2(5-2x)^2-2x(7x+12)\)
`= 5(4x^2 - 4x + 1) + 2(x^2 + 2x - 3) - 2(25 - 20x + 4x^2) - 14x^2 - 24x`
`= 20x^2 - 20x + 5 + 2x^2 + 4x - 6 - 50 + 40x - 8x^2 - 14x^2 - 24x`
`= - 51`
25 tháng 9 2023
`c)`
\(2(5x-1)(x^2-5x+1)+(x^2-5x+1)^2+(5x-1)^2-(x^2-1)(x^2+1)\)
`= [ 2(5x - 1) + x^2 - 5x + 1] * (x^2 - 5x + 1) + (5x - 1)^2 - [ (x^2)^2 - 1]`
`= (10x - 2 + x^2 - 5x + 1) * (x^2 - 5x + 1) + (5x - 1)^2 - x^4 + 1`
`= (x^2 + 5x - 1)(x^2 - 5x + 1) + (5x - 1)^2 - x^4 + 1`
`= x^4 - (5x - 1)^2 + (5x - 1)^2 - x^4 + 1`
`= 1`
`d)`
\((x^2+4)^2-(x^2+4)(x^2-4)(x^2+16)-8(x-4)(x+4)\)
`= (x^2 + 4)*[x^2 + 4 - (x^2 - 4)(x^2 + 16)] - 8(x^2 - 16)`
`= (x^2 + 4)(x^4 + 12x^2 - 64) - 8x^2 + 128`
`= x^6 + 16x^4 - 16x^2 - 256 - 8x^2 + 128`
`= x^6 + 16x^4 - 24x^2 - 128`
12 tháng 9 2021
a) \(A=x^2+3x+4=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
\(minA=\dfrac{7}{4}\Leftrightarrow x=-\dfrac{3}{2}\)
b) \(B=2x^2-x+1=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)
\(minB=\dfrac{7}{8}\Leftrightarrow x=\dfrac{1}{4}\)
c) \(C=5x^2+2x-3=5\left(x+\dfrac{1}{5}\right)^2-\dfrac{16}{5}\ge-\dfrac{16}{5}\)
\(minC=-\dfrac{16}{5}\Leftrightarrow x=-\dfrac{1}{5}\)
d) \(D=4x^2+4x-24=\left(2x+1\right)^2-25\ge-25\)
\(minD=-25\Leftrightarrow x=-\dfrac{1}{2}\)
e) \(E=x^2+6x-11=\left(x+3\right)^2-20\ge-20\)
\(minE=-20\Leftrightarrow x=-3\)
f) \(G=\dfrac{1}{4}x^2+x-\dfrac{1}{3}=\left(\dfrac{1}{2}x+1\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\)
\(minG=-\dfrac{4}{3}\Leftrightarrow x=-2\)
12 tháng 9 2021
\(A=x^2+3x+4=\left(x^2+3x+\dfrac{9}{4}\right)+\dfrac{7}{4}=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\)
Do \(\left(x+\dfrac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
\(minA=\dfrac{7}{4}\Leftrightarrow x+\dfrac{3}{2}=0\Leftrightarrow x=-\dfrac{3}{2}\)
Mấy câu còn lại làm tương tự nhé em^^
TN
1
KV
26 tháng 12 2023
a) (x - 2).3⁵ = 3⁷
x - 2 = 3⁷ : 3⁵
x - 2 = 3²
x - 2 = 9
x = 9 + 2
x = 11
b) x² - 2x = 0
x(x - 2) = 0
⇒ x = 0 hoặc x - 2 = 0
*) x - 2 = 0
x = 2
Vậy x = 0; x = 2
c) (2x - 1)² = 49
⇒ 2x - 1 = 7 hoặc 2x - 1 = -7
*) 2x - 1 = 7
2x = 7 + 1
2x = 8
x = 8 : 2
x = 4
*) 2x - 1 = -7
2x = -7 + 1
2x = -6
x = -6 : 2
x = -3
Vậy x = -3; x = 4
|x2+|6x - 2|| = x2+ 4
x2+|6x-2| = x2+4
| 6x -2| =x2+4-x2
|6x - 2 | = 4
\(\Rightarrow\left[{}\begin{matrix}6x-2=4\\6x-2=-4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}6x=6\\6x=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-1}{3}\end{matrix}\right.\)
vậy...
đây là TH1 thui mk cần TH2 cơ