Câu 9:Cho thỏa mãn điều kiện
Vậy giá trị nhỏ nhất của
là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Phương pháp:
Rút y theo x từ phương trình (1), thế vào phương trình (2) để tìm khoảng giá trị của x.
Đưa biểu thức P về 1 ẩn x và tìm GTLN, GTNN của biểu thức P.
Cách giải: 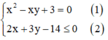
Ta nhận thấy x = 0 không thỏa mãn phương trình (1), do đó 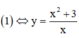 thế vào (2):
thế vào (2):
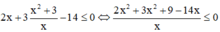
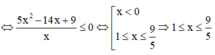
![]()
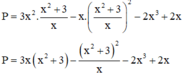
Sử dụng MTCT ta tính được
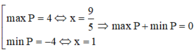

Áp dụng BĐT (a - b)² ≥ 0 → a² + b² ≥ 2ab ta có:
+) x² + y² ≥ 2xy
x² + 1 ≥ 2x
+) y² + z² ≥ 2yz
y² + 1 ≥ 2y
+) z² + x² ≥ 2xz
z² + 1 ≥ 2z
=> 2 ( x2 + y2 + z2 ) ≥ 2( xy + yz + xz )
cộng các BĐT trên ta có
3( x2 + y2 + z2 ) + 3 ≥ 2( x + y + z + xy + yz + xz)
=> GTNN của P = 3 khi và chỉ khi x=y=z=1

x + y = 1 => y = 1 - x
A = x3 + y3 = (x + y)(x2 - xy + y2)
= x2 - x(1 - x) + (1 - x)2
= x2 - x + x2 + x2 - 2x + 1
= 3x2 - 3x + 1
= 3(x2 - x + \(\dfrac{1}{3}\))
= 3(x2 - 2x.\(\dfrac{1}{2}\) + \(\dfrac{1}{4}+\dfrac{1}{12}\))
= 3(x - \(\dfrac{1}{2}\))2 + \(\dfrac{1}{4}\) ≥ \(\dfrac{1}{4}\) ∀x
Dấu "=" xảy ra ⇔ x - \(\dfrac{1}{2}\) = 0 ⇔ x = \(\dfrac{1}{2}\)
Vậy minA = \(\dfrac{1}{4}\) ⇔ x = \(\dfrac{1}{2}\)

Đáp án A
Gọi z = x + i y , x , y ∈ ℝ
z - 1 - i = 1 ⇔ x + i y - 1 - i = 1
⇔ x - 1 2 + y - 1 2 = 1 2 C
Gọi I là tâm của đường tròn (C).
Với mọi điểm P bất kì chạy trên S,
ta có O P ≤ O M + M P
do đó số phức tương ứng với P có môđun lớn nhất
khi và chỉ khi OP lớn nhất
OP = OM + MP
Tương đương 3 điểm O, M, P thẳng hàng
và M nằm giữa O và P
⇔ P ≡ P ' x P > 1
Phương trình đường thẳng OI: y = x
Tọa độ P’ là nghiệm của hệ phương trình :


Ta có
\(A=\dfrac{4}{x+1}+\dfrac{9}{y+2}+\dfrac{25}{z+3}\)
\(A=\dfrac{2^2}{x+1}+\dfrac{3^2}{y+2}+\dfrac{5^2}{z+3}\)
\(A\ge\dfrac{\left(2+3+5\right)^2}{x+1+y+2+z+3}\) (BĐT Schwarz)
\(A\ge\dfrac{10^2}{10}=10\) (vì \(x+y+z=4\))
ĐTXR \(\Leftrightarrow\dfrac{2}{x+1}=\dfrac{3}{y+2}=\dfrac{5}{z+3}\)
\(\Rightarrow\dfrac{2}{x+1}=\dfrac{3}{y+2}=\dfrac{5}{z+3}=\dfrac{2+3+5}{z+1+y+2+z+3}=1\). Dẫn đến \(\left\{{}\begin{matrix}x=1\\y=1\\z=2\end{matrix}\right.\). Vậy, GTNN của A là 10 khi \(\left(x,y,z\right)=\left(1,1,2\right)\)
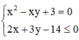 Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu
Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu 
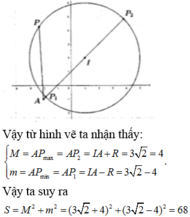
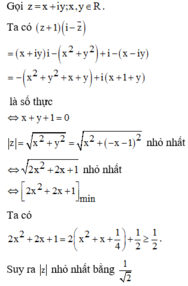
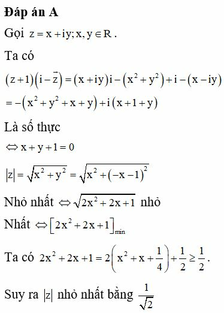
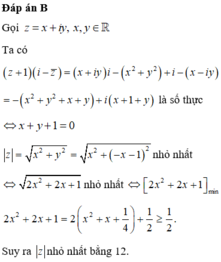
Ta có:
\(x^2+1\ge2x\)
\(y^2+1\ge2y\)
\(z^2+1\ge2z\)
\(2\left(x^2+y^2+z^2\right)\ge2\left(xy+yz+xz\right)\)
Cộng các BĐT vào ta có:
\(3\left(x^2+y^2+z^2\right)+3\ge2\left(x+y+z+xy+yz+xz\right)\)
\(3\left(x^2+y^2+z^2\right)+3\ge12\)
\(3\left(x^2+y^2+z^2\right)\ge9\)
\(x^2+y^2+z^2\ge3\)
Vậy: MinP = 3
3