Cho tam giác ABC có 3 góc nhọn. Xác định vị tri của điểm M trong tam giác sao cho MA+MB+MC nhỏ nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 2 2019
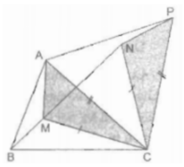
Trong ∆ ABC ta lấy điểm M. Nối MA, MB, MC.
Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.
Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.
Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Khi đó, CA = CP
Xét ∆ AMC và ∆ PNC:
CM = CN (vì ΔMCN đều)
CA = CP (vì ΔAPC đều)
Suy ra: ∆ AMC = ∆ PNC (c.g.c)
⇒ PN = AM
MA + MB + MC = NP + MB + MN
Ta có ∆ ABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.
7 tháng 8 2016
Ta dựng các tam giác đều AMP , AMN , ACE , ABD , suy ra N,P,E,D cố định.
Dễ dàng chứng minh được \(\Delta APE=\Delta AMC\left(c.g.c\right)\)
\(\Rightarrow MC=PE\), \(AM=MP\)
Suy ra : \(AM+MC+BM=BM+MP+PE\ge BE\)(hằng số)
Tương tự , ta cũng chứng minh được \(AM=MN\), \(BM=DN\)
\(\Rightarrow AM+MC+MB=CM+MN+DN\ge CD\)(hằng số)
Suy ra MA + MB + MC đạt giá trị nhỏ nhất khi M là giao điểm của BE và CD.
Cần chú ý : Vì điều kiện các góc của tam giác nhỏ hơn 180 độ :
\(\widehat{BAC}+\widehat{CAE}< 120^o+60^o=180\)
\(\widehat{BAC}+\widehat{BAD}< 120^o+60^o=180^o\)
nên BE cắt AC tại một điểm nằm giữa A và C , CD cắt AB tại một điểm nằm giữa A và B. Do đó tồn tại giao điểm M của CD và BE.
24 tháng 2 2019
a) Xét \(\Delta MBD\)và \(\Delta MAC\)
có: \(\widehat{MAC}=\widehat{MBD}\)( cùng chắn cung MC)
\(\widehat{BMD}=\widehat{AMC}\)( cung AB=cung AC vì AB=AC)
=> \(\Delta MBD\)~ \(\Delta MAC\)
b) Từ câu a)_
=> \(\frac{MB}{MA}=\frac{BD}{AC}\)(1)
\(\frac{MC}{MA}=\frac{MD}{MB}\)(2)
Dễ dàng chứng minh đc:
\(\Delta BDM~\Delta ADC\)
=> \(\frac{MD}{MB}=\frac{DC}{AC}\)(3)
Từ (1), (2), (3)
=> \(\frac{MB}{MA}+\frac{MC}{MA}=\frac{BD}{AC}+\frac{CD}{AC}=\frac{BC}{AC}\)\(=\frac{BC}{AB}\)
c) Lấy điểm E thuộc đoạn
14 tháng 9 2023
Ta thấy \(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}=\overrightarrow{CM}\)
Như vậy, điểm M chính là đỉnh thứ tư của hình bình hành ABCM.
Trước tiên ta phát biểu và chứng minh một bổ đề:
Bổ đề. "Cho tam giác ABCABC và một điểm MM nằm trong tam giác. Chứng minh rằng MB+MC<AB+ACMB+MC<AB+AC."
Chứng minh. Kéo dài BMBM về phía MM cắt cạnh ACAC tại điểm NN. Theo bất đẳng thức tam giác ta có:
$$AN+AB>BN=BM+MN\\
MN+NC>MC$$
Cộng theo vế các bất đẳng thức trên và trừ đi hai vế cho MNMN ta thu được bất đẳng thức cần chứng minh.
Ta xét hai trường hợp:
a) Tam giác ABCABC có ba góc nhỏ hơn 120∘120∘.
Ta dựng tam giác đều BCDBCD ở phía ngoài tam giác ABCABC.
Gọi TT là giao điểm của đường tròn ngoại tiếp tam giác BCDBCD với ADAD. Dễ dàng chứng minh rằng TT nhìn ba cạnh của tam giác ABCABC dưới ba góc bằng nhau. Ta chứng minh rằng với một điểm MM tùy ý ở trong tam giác ABCABC khác điểm TT thì ta cóMA+MB+MC>TA+TB+TCMA+MB+MC>TA+TB+TC
Thật vậy ta có MB+MC≥MDMB+MC≥MD và do đóMA+MB+MC≥MA+MD≥AD (1)MA+MB+MC≥MA+MD≥AD (1)
Mặt khác TA+TB+TC=TA+TDTA+TB+TC=TA+TD, do TT nằm trên đường tròn ngoại tiếp tam giác đều BCDBCD. Và cuối cùng làTA+TB+TC=TA+TD=AD (2)TA+TB+TC=TA+TD=AD (2)
Từ (1)(1) và (2)(2) suy raMA+MB+MC≥TA+TB+TCMA+MB+MC≥TA+TB+TC
Đẳng thức xảy ra khi M≡TM≡T (điểm TT được gọi là điểm Toricenli của tam giác ABCABC).
b) Tam giác ABCABC có một góc, chẳng hạn ˆB≥120∘B^≥120∘.
Dựng tam giác đều BCDBCD ở phía ngoài của tam giác ABCABC.
Do ˆB≥120∘B^≥120∘ nên với mọi điểm MM tùy ý ở trong tam giác ABCABC, điểm BB nằm trong tam giác MDAMDA.
Ta có MB+MC≥MDMB+MC≥MD. Mặt khác theo bổ đề trên đối với tam giác MDAMDA ta có MA+MD≥BA+BDMA+MD≥BA+BD.
Từ đó ta cóOA+OB+OC≥OA+OD≥BA+BD=BA+BCOA+OB+OC≥OA+OD≥BA+BD=BA+BC
Như vậy khi M≡BM≡B thì tổng khoảng cách từ MM đến các đỉnh còn lại của tam giác ABCABC là nhỏ nhất. Tóm lại trong trường hợp tam giác ABCABC có một đỉnh không nhỏ hơn 120∘120∘ thì chỉnh đỉnh này là đỉnh cần tìm.
thanks nhìu nha!!!