Giúp mình bài III...
Đọc tiếp
Giúp mình bài III nha!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
10 tháng 9 2018
Soạn bài từ mượn
I. Từ thuần Việt và từ mượn Học sinh dựa vào từ điển tiếng Việt để giải thích :
1. - Trượng. - Tráng sĩ.
2. Các từ trên có nguồn gốc từ ngôn ngữ Hán.
3. Những từ tiếng Hán : sứ giả, điệu, giang sơn. Những từ mượn các ngôn ngữ khác : tivi, xà phòng, mít ting, ra-đi-ô, ga, Xô-viết, in-tơ-nét.
4. - Với các từ mượn từ đã Việt hóa chúng ta viết như từ thuần Việt. - Với các từ mượn chưa Việt hóa (tiếng châu Âu) chúng ta nên dùng dấu gạch ngang giữa các tiếng.
II. Nguyên tắc mượn từ.
1. Mượn từ để làm giàu tiếng Việt
2. Không nên mượn từ nước ngoài tùy tiện.
III. Luyện tập
Câu 1. - Những từ mượn từ tiếng Hán. + Vô cùng ; tự hiên ; sính lễ. + Gia nhân. + Quyết định ; lãnh địa. - Những từ mượn tiếng châu Âu : lốp, in-tơ-nét.
Câu 2. Hãy xác định nghĩa của các tiếng tạo thành các từ Hán Việt dưới đây. a. - Giả : tiếng dùng để chỉ người hay vật, ở đây là người, kẻ. - Khán : nhìn trông coi. - Thính : nghe. - Độc : đọc b. - Yếu : quan trọng, cần gấp. - Điểm : vết đen, cái chấm, là điểm. - Lược : tóm tắt những điều cơ bản, chủ yếu. - Nhân : người.
Câu 3. Kể một số từ mượn : a. Mét, ki-lô-mét, xen-ti-mét, ki-lô-gam, lít, đấu (thóc), tá (bút)… b. Ghi đông, phuốc-tăng, đĩa xiđi…
Câu 4. - Đó là : phôn, fan, nốc ao. - Dùng những từ này trong giao tiếp sinh hoạt với những bạn bè của mình.
Câu 5. Chép chính tả lưu ý các từ mượn.
10 tháng 9 2018
bạn cũng có thể tham khảo trong sách để học tốt ngữ văn 6 nha!
#khoa#
NV
30 tháng 10 2021
friends - listening - English - teacher
watching - stories - pen - club
TG
giải giúp mình bài II vs III ạ mình làm rồi nhưng sợ sai (4 điểm)
2
11 tháng 2 2022
Bài II, câu 3 chọn I
4 - high
5 - ride
6 - put it on
7 - happy
9 - looking
10 - not to smoke
Bài III
2 - C
4 - A
TM
6 tháng 4 2023
Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
TM
6 tháng 4 2023
Bài IV.b.
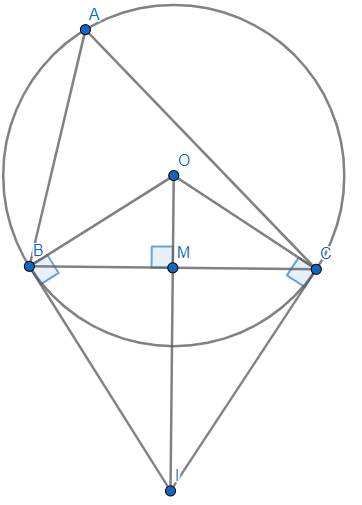
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
IM
18 tháng 8 2016
III. What are these places?
??????
Mình 0 hỉu cái topic này
=))
