Giải phương trình
(x2 + x )2 + 4(x2 + x ) - 12 = 0
HELP ME 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
13 tháng 12 2018
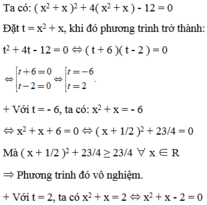
⇔ ( x + 2 )( x - 1 ) = 0 ⇔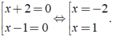 
Vậy phương trình có tập nghiệm là S = { - 2;1 }.
AH
Akai Haruma
Giáo viên
31 tháng 1 2023
Bài 1:
$2x^4-3x^2-5=0$
$\Leftrightarrow (2x^4+2x^2)-(5x^2+5)=0$
$\Leftrightarrow 2x^2(x^2+1)-5(x^2+1)=0$
$\Leftrightarrow (x^2+1)(2x^2-5)=0$
$\Leftrightarrow 2x^2-5=0$ (do $x^2+1\geq 1>0$ với mọi $x\in\mathbb{R}$)
$\Leftrightarrow x^2=\frac{5}{2}$
$\Leftrightarrow x=\pm \sqrt{\frac{5}{2}}$
AH
Akai Haruma
Giáo viên
31 tháng 1 2023
Bài 2:
a. Khi $m=1$ thì pt trở thành:
$x^2-6x+5=0$
$\Leftrightarrow (x^2-x)-(5x-5)=0$
$\Leftrightarrow x(x-1)-5(x-1)=0$
$\Leftrightarrow (x-1)(x-5)=0$
$\Leftrightarrow x-1=0$ hoặc $x-5=0$
$\Leftrightarrow x=1$ hoặc $x=5$
b.
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta=(m+5)^2-4(-m+6)\geq 0$
$\Leftrightarrow m^2+14m+1\geq 0(*)$
Áp dụng định lý Viet:
$x_1+x_2=m+5$
$x_1x_2=-m+6$
Khi đó:
$x_1^2x_2+x_1x_2^2=18$
$\Leftrightarrow x_1x_2(x_1+x_2)=18$
$\Leftrightarrow (m+5)(-m+6)=18$
$\Leftrightarrow -m^2+m+12=0$
$\Leftrightarrow m^2-m-12=0$
$\Leftrightarrow (m+3)(m-4)=0$
$\Leftrightarrow m=-3$ hoặc $m=4$
Thử lại vào $(*)$ thấy $m=4$ thỏa mãn.
PT
20 tháng 3 2022
a) x(4x + 2) = 4x2 - 14
⇔ 4x2 + 2x = 4x2 - 14
⇔ 4x2 - 4x2 + 2x = -14
⇔ 2x = -14
⇔ x = -7
Vậy tập nghiệm S = ......
b) (x2 - 9)(2x - 1) = 0
⇔ x2 - 9 = 0 hoặc 2x - 1 = 0
⇔ x2 = 9 hoặc 2x = 1
⇔ x = 3 hoặc -3 hoặc x = \(\dfrac{1}{2}\)
Vậy .......
c) \(\dfrac{3}{x-2}\) + \(\dfrac{4}{x+2}\) = \(\dfrac{x-12}{x^2-4}\)
⇔ \(\dfrac{3}{x-2}\) + \(\dfrac{4}{x+2}\) = \(\dfrac{x-12}{\left(x-2\right)\left(x+2\right)}\)
ĐKXĐ: x - 2 ≠ 0 và x + 2 ≠ 0
⇔ x ≠ 2 và x ≠ -2MSC (mẫu số chung): (x - 2)(x + 2)Quy đồng mẫu hai vế và khử mẫu ta được:3x + 6 + 4x - 8 = x - 12⇔ 3x + 4x - x = 8 - 6 - 12⇔ 6x = -10⇔ x = \(-\dfrac{5}{3}\) (nhận)Vậy ........
A4
2
H
23 tháng 2 2023
`a,x^2 +4x-5=0`
`<=> x^2-x+5x-5=0`
`<=> x(x-1)+5(x-1)=0`
`<=>(x-1)(x+5)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-5\end{matrix}\right.\)
`b, x^2 -x-12=0`
`<=> x^2 +3x-4x-12=0`
`<=>(x^2+3x)-(4x+12)=0`
`<=>x(x+3)-4(x+3)=0`
`<=>(x+3)(x-4)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=4\end{matrix}\right.\)
`c, (2x-7)^2 - 6(2x-7)(x-3)=0`
`<=>(2x-7)(2x-7 -6x+18)=0`
`<=>(2x-7) ( -4x+11)=0`
\(\Leftrightarrow\left[{}\begin{matrix}2x-7=0\\-4x+11=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=7\\-4x=-11\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=\dfrac{11}{4}\end{matrix}\right.\)
23 tháng 2 2023
a: =>(x+5)(x-1)=0
=>x=1 hoặc x=-5
b: =>(x-4)(x+3)=0
=>x=4 hoặc x=-3
c: =>(2x-7)(2x-7-6x+18)=0
=>(2x-7)(-4x+11)=0
=>x=11/4 hoặc x=7/2
NN
2
Y
11 tháng 4 2022
\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow x-1< 3\)
\(\Leftrightarrow x< 4\)
\(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(2+x\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2-x=0\\2+x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-2\end{matrix}\right.\)
\(\dfrac{x+2}{x-5}< 0\)
\(\Leftrightarrow x+2< 0\)
\(\Leftrightarrow x< -2\)
11 tháng 4 2022
a)\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow\left(x-1\right)^2-9< 0\)
\(\Leftrightarrow\left(x-1-3\right)\left(x-1+3\right)< 0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4< 0\\x+2>0\end{matrix}\right.hay\left[{}\begin{matrix}x-4>0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 4\\x>-2\end{matrix}\right.hay\left[{}\begin{matrix}x>4\\x< -2\end{matrix}\right.\)(vô lý)
-Vậy nghiệm của BĐT là \(-2< x< 4\).
b) \(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(x+2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+2\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1< 0\\x-2>0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2< 0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2 >0\\x+2< 0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1< 0\\x-2< 0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>2\\x>-2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x>1\\x< 2\\x>-2\end{matrix}\right.\) (có thể xảy ra) hay
\(\left[{}\begin{matrix}x>1\\x>2\\x< -2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x< 1\\x< 2\\x< -2\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(x< -2\) hay \(1< x< 2\).
c) ĐKXĐ: \(x\ne5\)
\(\dfrac{x+2}{x-5}< 0\Leftrightarrow\left[{}\begin{matrix}x+2< 0\\x-5>0\end{matrix}\right.hay\left[{}\begin{matrix}x+2>0\\x-5< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -2\\x>5\end{matrix}\right.\)(vô lí) hay
\(\left[{}\begin{matrix}x>-2\\x< 5\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(-2< x< 5\)
AH
Akai Haruma
Giáo viên
24 tháng 8 2023
1. Đặt $x^2+x=a$ thì pt trở thành:
$a^2+4a=12$
$\Leftrightarrow a^2+4a-12=0$
$\Leftrightarrow (a-2)(a+6)=0$
$\Leftrightarrow a-2=0$ hoặc $x+6=0$
$\Leftrightarrow x^2+x-2=0$ hoặc $x^2+x+6=0$
Dễ thấy $x^2+x+6=0$ vô nghiệm.
$\Rightarrow x^2+x-2=0$
$\Leftrightarrow (x-1)(x+2)=0$
$\Leftrightarrow x=1$ hoặc $x=-2$
AH
Akai Haruma
Giáo viên
24 tháng 8 2023
2.
$x(x-1)(x+1)(x+2)=24$
$\Leftrightarrow [x(x+1)][(x-1)(x+2)]=24$
$\Leftrightarrow (x^2+x)(x^2+x-2)=24$
$\Leftrightarrow a(a-2)=24$ (đặt $x^2+x=a$)
$\Leftrightarrow a^2-2a-24=0$
$\Leftrightarrow (a+4)(a-6)=0$
$\Leftrightarrow a+4=0$ hoặc $a-6=0$
$\Leftrightarrow x^2+x+4=0$ hoặc $x^2+x-6=0$
Nếu $x^2+x+4=0$
$\Leftrightarrow (x+\frac{1}{2})^2=\frac{1}{4}-4<0$ (vô lý - loại)
Nếu $x^2+x-6=0$
$\Leftrightarrow (x-2)(x+3)=0$
$\Leftrightarrow x-2=0$ hoặc $x+3=0$
$\Leftrightarrow x=2$ hoặc $x=-3$
CB
1
AH
Akai Haruma
Giáo viên
12 tháng 2 2023
Lời giải:
Đặt $x^2+x=a$ thì pt trở thành:
$(a-2)(a-3)=12$
$\Leftrightarrow a^2-5a+6=12$
$\Leftrightarrow a^2-5a-6=0$
$\Leftrightarrow (a+1)(a-6)=0$
$\Leftrightarrow a+1=0$ hoặc $a-6=0$
$\Leftrightarrow x^2+x+1=0$ hoặc $x^2+x-6=0$
Nếu $x^2+x+1=0$
$\Leftrightarrow (x+\frac{1}{2})^2=-\frac{3}{4}<0$ (vô lý - loại)
Nếu $x^2+x-6=0$
$\Leftrightarrow (x-2)(x+3)=0$
$\Leftrightarrow x=2$ hoặc $x=-3$
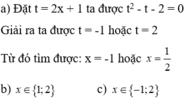
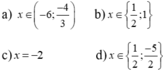
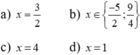
\(\left(x^2+x\right)^2+4\left(x^2+x\right)-12=0\)
\(\Leftrightarrow\left(x^2+x\right)^2+4\left(x^2+x\right)+4-16=0\)
\(\Leftrightarrow\left(x^2+x+2\right)^2-16=0\)
\(\Leftrightarrow\left(x^2+x-2\right)\left(x^2+x+6\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2+x+6\right)=0\)
vì \(\left(x^2+x+6\right)>0\) nên\(\left[{}\begin{matrix}x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Vậy tập nghiện của pt là:\(S=\left\{1;-2\right\}\)
Bạn ơi, mình không hiểu đoạn ( x2 + x + 2 )2 -16 = 0