Câu 9:Biết Giá trị nhỏ nhất của
là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TQ
5
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
4 tháng 1 2023
Lời giải:
Ta thấy: $x^2\geq 0$ với mọi $x$ nên $x^2+9+2019\geq 9+2019=2028$
$\Rightarrow A=\sqrt{x^2+9+2019}\geq \sqrt{2028}$
Vậy GTNN của $A$ là $\sqrt{2028}$ khi $x=0$
VT
2 tháng 12 2018
Chọn B.
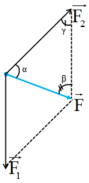
Theo định lí hàm số sin:
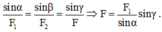
Vì không đổi, nên F nhỏ nhất khi sin = 1 => α = 90 °
8 tháng 5 2019
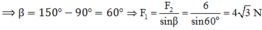
\(A=\frac{27-12x}{x^2+9}\)
\(A=\frac{x^2-12x+36-x^2-9}{x^2+9}\)
\(A=\frac{\left(x-36\right)^2-\left(x^2+9\right)}{x^2+9}\)
\(A=\frac{\left(x-36\right)^2}{x^2+9}-\frac{x^2+9}{x^2+9}\)
\(A=\frac{\left(x-36\right)^2}{x^2+9}-1\ge-1\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x=36\)
NQ
0
NQ
0
NQ
0
K
1
31 tháng 10 2015
trung bình cộng của a và 9a là:(9a+a):2=10a:2=5a chia hết cho 3
=>a chia hết cho 3
mà a nhỏ nhất nên a=3
**** b!
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(\dfrac{3x^2-1}{x^2+2}=\dfrac{6x^2-2}{2\left(x^2+2\right)}=\dfrac{7x^2-\left(x^2+2\right)}{2\left(x^2+2\right)}=\dfrac{7x^2}{2\left(x^2+2\right)}-\dfrac{1}{2}\ge=-\dfrac{1}{2}\)
GTNN của biểu thức là \(-\dfrac{1}{2}\), xảy ra khi \(x=0\)
Biểu thức ko tồn tại GTLN
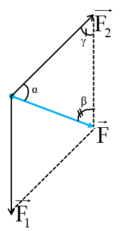
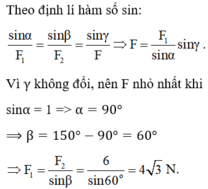
Áp dụng BĐT \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta có:
\(A=\left|x-2\right|+\left|y+3\right|=\left|x-2\right|+\left|-y-3\right|\)
\(\ge\left|x-2-y-3\right|=\left|x-y-5\right|=3\)
Dấu "=" xảy ra khi \(x=y+2\)
Vậy với \(x=y+2\) thì \(A_{Min}=3\)
mk đoán là 3 bạn nhé!