cho hình bình hành ABCD, trên đường phân giác trong của BAD lấy điểm P và trên đường phân giác trong của BCD lấy điểm Q sao cho PQ // AB. CMR ADP bằng ABQ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 2 2020
Em kiểm tra lại đề bài . Gọi P, Q là hình chiếu của K trên BC và gì nữa vậy?
KN
13 tháng 7 2020
Gọi N là giao điểm của PQ và AH, gọi M là giao điểm của AH với (O). Khi đó dễ thấy tam giác PHK cân. Do AH//KP nên tứ giác KPMN là hình thang.
Lại có BPKQ nội tiếp nên suy ra được \(\widehat{QBK}=\widehat{ABK}=\widehat{ AMK}=\widehat{QPK}\)nên tứ giác KPMN nội tiếp. Do đó KPMN là hình thang cân. Do đó \(\widehat{PMH}=\widehat{PHM}=\widehat{KNM}\)nên KN//HP.
Do vậy tứ giác HPKN là hình bình hành. Từ đó ta có điều phải chứng minh.
11 tháng 2 2020
Cảm ơn bạn vì đã có ý giúp nhưng mình tìm được câu tương tự rồi. Cảm ơn bạn nhiều
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
Trước hết ta chứng minh bổ đề sau (nếu em chưa học)
Cho 4 điểm A; B; C; D phân biệt sao cho \(AB||CD\), khi đó ta luôn có: \(S_{\Delta ACD}=S_{\Delta BCD}\)
C/m: từ A và B lần lượt kẻ \(AH\) và \(BK\) vuông góc CD \(\Rightarrow AH||BK\Rightarrow\) tứ giác AHKB là hình chữ nhật
\(\Rightarrow AH=BK\)
Do \(\left\{{}\begin{matrix}S_{\Delta ACD}=\dfrac{1}{2}AH.CD\\S_{\Delta BCD}=\dfrac{1}{2}BK.CD\end{matrix}\right.\) mà \(AH=BK\Rightarrow S_{\Delta ACD}=S_{\Delta BCD}\) (đpcm)
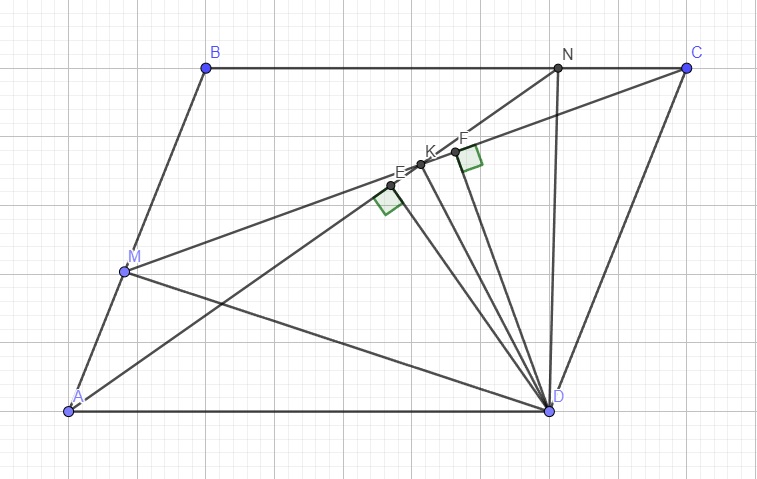
Quay lại bài toán, áp dụng bổ đề trên ta có: do N thuộc BC nên \(NC||AD\Rightarrow S_{\Delta NAD}=S_{\Delta CAD}\) (1)
Tương tự, \(AM||CD\Rightarrow S_{\Delta ACD}=S_{\Delta MCD}\) (2)
(1);(2) \(\Rightarrow S_{\Delta NAD}=S_{\Delta MCD}\)
Từ D lần lượt kẻ \(DE\perp AN\) và \(DF\perp CM\)
\(\Rightarrow\left\{{}\begin{matrix}S_{\Delta NAD}=\dfrac{1}{2}DE.AN\\S_{\Delta MCD}=\dfrac{1}{2}DF.CM\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}S_{\Delta NAD}=S_{\Delta MCD}\\AN=CM\end{matrix}\right.\) \(\Rightarrow DE=DF\)
\(\Rightarrow\Delta_VDEK=\Delta_VDFK\left(ch-cgv\right)\)
\(\Rightarrow\widehat{EKD}=\widehat{FKD}\) hay KD là phân giác
