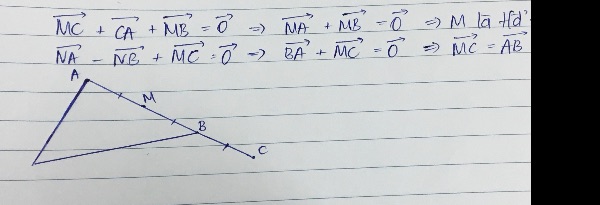1. Cho hình bình hành ABCD,M là điểm tùy ý.Đẳng thức vectơ nào sau đây đúng:
A. vectơ MA + vectơ MC + vectơ MD + vectơ MA = vectơ 0
B. vectơ MB + vectơ MC = vectơ MD + vectơ MA
C. vectơ MA +vectơ MC = vectơ MB + vectơ MD
D. vectơ MD +vectơ MC = vectơ MB + vectơ MA