Xét tính tăng giảm của các dãy số sau:
a) u1=15n-9
b) un=4n
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


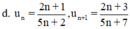
với n ∈ N*, n ≥ 1
Xét:
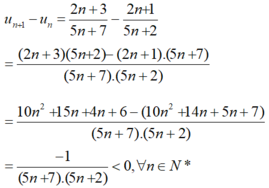
⇒ un + 1 – un < 0 ⇒ un + 1 < un
Vậy (un) là dãy số giảm

Chọn A.
Trước hết ta chứng minh 1 < un < 4
Điều này hiển nhiên đúng với n = 1.
Giả sử 1 < un < 4, ta có: ![]()
Ta chứng minh (un) là dãy tăng
Ta có u1 < u2, giả sử un-1 < un, ∀ n ≤ k.
Khi đó: 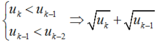
![]()
Vậy dãy (un) là dãy tăng và bị chặn.

Chọn B.
Trước hết bằng quy nạp ta chứng minh: (un) 1 < un ≤ 2, ∀ n
Điều này đúng với n = 2, giả sử 1 < un < 2 ta có: ![]() nên ta có đpcm.
nên ta có đpcm.
Mà ![]() .
.
Vậy dãy (un) là dãy giảm và bị chặn.

Ta có:
u n + 1 − u n = 3 ( n + 1 ) 2 − 2 ( n + 1 ) + 1 n + 2 − 3 n 2 − 2 n + 1 n + 1 = 3 n 2 + 4 n + 2 n + 2 − 3 n 2 − 2 n + 1 n + 1 = ( 3 n 2 + 4 n + 2 ) . ( n + 1 ) − ( 3 n 2 − 2 n + 1 ) . ( n + 2 ) ( n + 2 ) . ( n + 1 ) = 3 n 2 + 7 n n + 1 n + 2 > 0
nên dãy ( u n ) là dãy tăng
Chọn đáp án A
b) \(U_n=4^n\)
U1=4^1; U2=4^2=16
c/m:
Uk=4k
Uk+1=4k+1
\(U_{k+1}-U_k=4^{k+1}-4^k=4^k\left(4-1\right)=3.4^k>0\)
\(U_{k+1}>U_k\)
Vậy kết luận dãy trên tăng dần