Tổng của 3 góc x,y,z trong hình sau:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Tổng số đo các góc x,y,z của tam giác ban đầu bằng số đo của góc bẹt và bằng 180o.
14 tháng 6 2023
a:
Đối đỉnh: góc tMx và góc yMz; góc tMy và góc xMz
Kề bù: góc tMz và góc tMy; góc yMz và góc xMz
b: Kề bù: góc MNA và góc MNx; góc MAN và góc zAM
c: Đối đỉnh: góc AIB và góc MIN; góc AIM và góc BIN
Kề bù: góc AIB và góc AIM
góc MIN và góc BIN
CM
3 tháng 5 2018
Chọn C
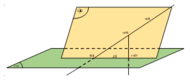
Ta có mặt phẳng α nhận vectơ n α → = ( 1 ; 1 ; 1 ) là vectơ pháp tuyến, đường thẳng d đi qua điểm A(0;-1;2) và nhận u d → = ( 1 ; 2 ; - 1 ) là vectơ chỉ phương.
Gọi β là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng α
Khi đó đường thẳng ∆ là giao tuyến của hai mặt phẳng α và β . Do đó một vectơ chỉ phương của đường thẳng ∆ là .
Mà u → = ( 1 ; a ; b ) nên a=4, b = -5 => a+b = 4-5 =-1.
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Số đơn thức đồng dạng với \({a^4}\) trong tổng là \(C_4^0 = 1\)
Số đơn thức đồng dạng với \({a^3}b\) trong tổng là \(C_4^4 = 1\)
Số đơn thức đồng dạng với \({a^2}{b^2}\) trong tổng là \(C_4^2 = 6\)
Số đơn thức đồng dạng với \(a{b^3}\) trong tổng là \(C_4^3 = 1\)
Số đơn thức đồng dạng với \({b^4}\) trong tổng là \(C_4^4 = 1\)
360o
Tổng số đo góc ngoài của tam giác bằng 360 độ