Question

[Nguyễn Thị Ngọc Bảo]

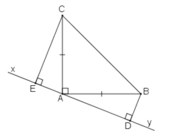
1. Cho tam giác ABC có góc A bằng 90 độva AB=AC .Qua A kẻ đường thẳng d sao cho BC nằm cùng phía đối với d .Kẻ BD và CE vuông góc với d(DE thuộc d)

Chứng minh rằng BD=AEvà AD=CE

2. Cho tam giác ABC nhọn . Gọi M là trung điểm của cạnh AC . Trên tia đối MB lấy D sao cho MD=MB.

a.Chứng minh :t/g ABM=t/g CDM

b. Chứng minh :AD//BC

c. Gọi N là trung điểm của BC đường thẳng NM cắt AD tại E Chứng minh M là trung điểm của NE

Giups minh nhé các bạn!

Answer 1

[Hoàng Thị Ngọc Anh]

a) Xét \(\Delta\)ABM và \(\Delta\)CDM có:

AM = CM (suy từ giả thiết)

\(\widehat{AMB}\) = \(\widehat{CMD}\) (đối đỉnh)

BM = DM (giả thiết)

=> \(\Delta\)ABM = \(\Delta\)CDM (c.g.c)

b) Xét \(\Delta\)AMD và \(\Delta\)CMB có:

AM = CM (suy từ gt)

\(\widehat{AMD}\) = \(\widehat{CMB}\) (đối đỉnh)

MD = MB (gt)

=> \(\Delta\)AMD = \(\Delta\)CMB (c.g.c)

=> \(\widehat{ADM}\) = \(\widehat{CBM}\) (2 góc tương ứng)

mà 2 góc ở vị trí so le trong nên AD // BC.

c) Vì \(\Delta\)AMD = \(\Delta\)CMB (câu b)

nên \(\widehat{ADM}\) = \(\widehat{CBM}\) (2 góc tương ứng)

hay \(\widehat{EDM}\) = \(\widehat{NBM}\)

Xét \(\Delta\)EDM và \(\Delta\)NBM có:

\(\widehat{EDM}\) = \(\widehat{NBM}\) (chứng minh trên)

DM = BM (gt)

\(\widehat{EMD}\) = \(\widehat{NMB}\) (đối đỉnh)

=> \(\Delta\)EDM = \(\Delta\)NBM (g.c.g)

=> EM = NM (2 cạnh tương ứng)

Do đó M là trung điểm của NE.

Answer 2

[Hoàng Thị Ngọc Anh]

Câu mk làm là câu 2, còn câu 1 làm ở phần kia nha