
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1 leaves
2 speaking
3 famous
4 nationality
5 more
6 different
7 worst
8 thirtieth
9 swimming
10 activities
1.leaves
2.speaking
3.famous
4.nationality
5.more
6.Differ
7.Badly
8.Thirty
9.Swimming
10.Act
Mik ko biết đúng hay ko nha

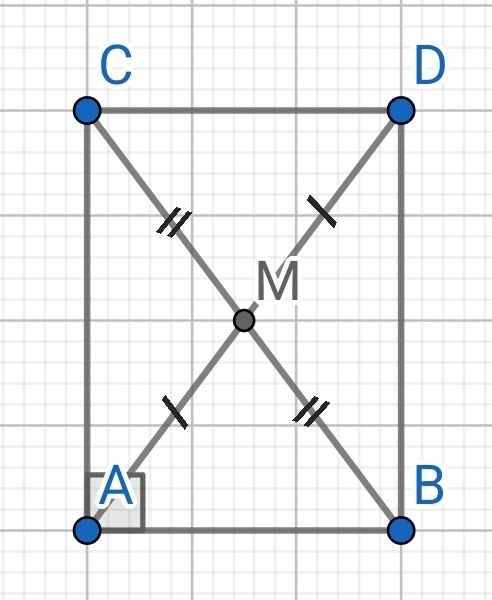
a) Do AM là đường trung tuyến của ∆ABC
⇒ M là trung điểm BC
Do MA = MD (gt)
⇒ M là trung điểm AD
Tứ giác ABDC có:
M là trung điểm BC (cmt)
M là trung điểm AD (cmt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (gt)
⇒ ABDC là hình chữ nhật
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC
⇒ AM = BC : 2
= 10 : 2
= 5 (cm)
c) Nếu ∠B = 45⁰
⇒ C = 90⁰ - ∠B
= 90⁰ - 45⁰
= 45⁰
⇒ ∆ABC vuông cân tại A
⇒ AB = AC
Lại có ABDC là hình chữ nhật
⇒ ABDC là hình vuông

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)

Lời giải:
$x+y+z=0\Rightarrow x+y=-z$. Khi đó:
$x^2+y^2-z^2=(x+y)^2-2xy-z^2=(-z)^2-2xy-z^2=-2xy$
Tương tự: $y^2+z^2-x^2=-2yz, z^2+x^2-y^2=-2xz$
Khi đó:
$A=\frac{xy}{-2xy}+\frac{yz}{-2yz}+\frac{zx}{-2zx}=\frac{1}{-2}+\frac{1}{-2}+\frac{1}{-2}=\frac{-3}{2}$

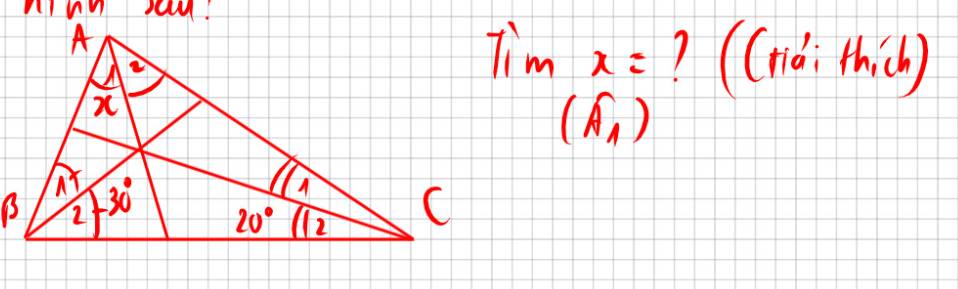
Vẽ lại hình:
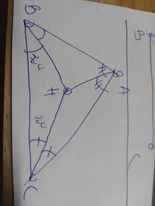
Theo hình vẽ, ta có: AH,BH,CH lần lượt là phân giác của góc BAC, góc ABC, góc ACB
BH là phân giác của góc ABC
=>\(\widehat{ABC}=2\cdot\widehat{HBC}=60^0\)
CH là phân giác của góc ACB
=>\(\widehat{ACB}=2\cdot\widehat{HCB}=2\cdot20^0=40^0\)
Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{BAC}+60^0+40^0=180^0\)
=>\(\widehat{BAC}=80^0\)
AH là phân giác của góc BAC
=>\(\widehat{BAH}=\widehat{CAH}=\dfrac{80^0}{2}=40^0\)
=>\(x=40^0\)

Bài 1
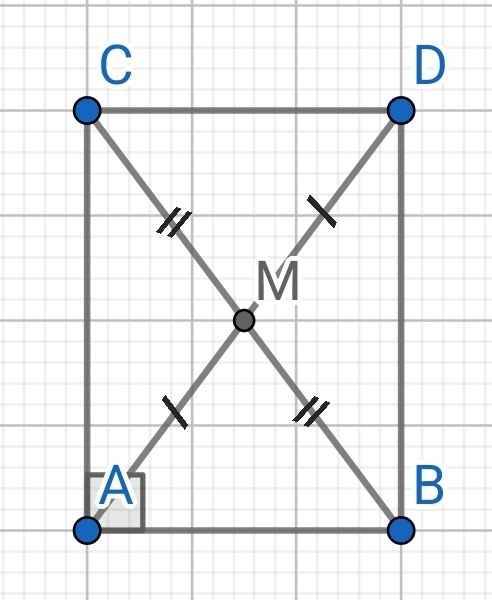 a) Do AM là đường trung tuyến của ∆ABC
a) Do AM là đường trung tuyến của ∆ABC
⇒ M là trung điểm BC
Do MA = MD (gt)
⇒ M là trung điểm AD
Tứ giác ABDC có:
M là trung điểm BC (cmt)
M là trung điểm AD (cmt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (gt)
⇒ ABDC là hình chữ nhật
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC
⇒ AM = BC : 2
= 10 : 2
= 5 (cm)
c) Nếu ∠B = 45⁰
⇒ C = 90⁰ - ∠B
= 90⁰ - 45⁰
= 45⁰
⇒ ∆ABC vuông cân tại A
⇒ AB = AC
Lại có ABDC là hình chữ nhật
⇒ ABDC là hình vuông
Bài 2
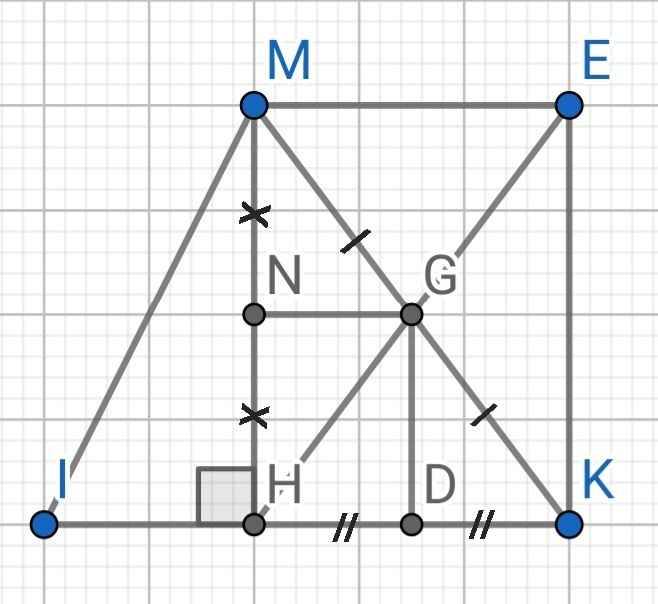 a) Do H và E đối xứng với nhau qua G (gt)
a) Do H và E đối xứng với nhau qua G (gt)
⇒ G là trung điểm của HE
Tứ giác MEKH có:
G là trung điểm HE (cmt)
G là trung điểm MK (gt)
⇒ MEKH là hình bình hành
Mà ∠MHK = 90⁰ (MH ⊥ IK)
⇒ MEKH là hình chữ nhật
b) ∆MHK có:
N là trung điểm MH (gt)
G là trung điểm MK (gt)
⇒ NG là đường trung bình của ∆MHK
⇒ NG // HK và NG = HK : 2
Do D là trung điểm HK
⇒ HD = HK : 2
⇒ HD = NG = HK : 2
Do NG // HK
⇒ NG // HD
Do ∠MHK = 90⁰
⇒ ∠NHD = 90⁰
Tứ giác NGDH có:
NG // HD (cmt)
NG = HD (cmt)
⇒ NGDH là hình bình hành
Mà ∠NHD = 90⁰ (cmt)
⇒ NGDH là hình chữ nhật








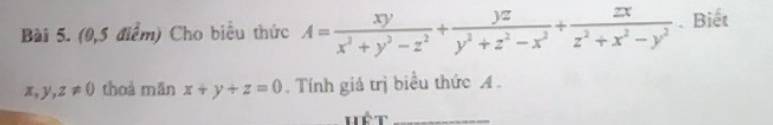

\(H=x^2+2y^2+\frac{1}{x}+\frac{24}{y}=x^2+1+2y^2+8+\frac{1}{x}+\frac{24}{y}-9\)
\(\ge2x+8y+\frac{1}{x}+\frac{24}{y}-9=x+\frac{1}{x}+6y+\frac{24}{y}+x+2y-9\)
\(\ge2.1+2.12+5-9=22\)
Dấu \(=\)khi \(x=1,y=2\).
Giải rõ ra giùm tôi được ko chứ tôi ko hiểu