Giải bft (lập bảng xét dấu nếu cần)
\(\left(x+1\right)\left(x-3\right)< 2\sqrt{x^2-2x-3}+3\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2) ĐK: \(x^2+5x+2\ge0\Leftrightarrow\left[\begin{array}{nghiempt}x\le\frac{-5-\sqrt{17}}{2}\\x\ge\frac{-5+\sqrt{17}}{2}\end{array}\right.\)
bpt \(\Leftrightarrow x^2+5x+4-3\sqrt{x^2+5x+2}< 6\)
Đặt \(t=\sqrt{x^2+5x+2}\left(t\ge0\right)\) , bất pt trở thành:
\(t^2+2-3t< 6\Leftrightarrow t^2-3t-4< 0\Leftrightarrow-1< t< 4\)
Kết hợp điều kiện được: \(0\le t< 4\Rightarrow0\le\sqrt{x^2+5x+2}< 4\Leftrightarrow x^2+5x+2< 16\)
\(\Leftrightarrow x^2+5x-14< 0\Leftrightarrow-7< x< 2\)
Kết hợp điều kiện, bất pt đã cho có tập nghiệm:
(-7; \(\frac{-5-\sqrt{17}}{2}\)] \(\cup\) [ \(\frac{-5+\sqrt{17}}{2}\); 2)

\(\left(x-2\right)\left(2x+3\right)< 0\)
\(\Leftrightarrow\left(x-2\right)\) và \(\left(2x+3\right)\) trái dấu .
Mà : \(\left(2x+3\right)>\left(x-2\right)\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}2x+3>0\\x-2< 0\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x>\frac{-3}{2}\\x< 2\end{array}\right.\)
\(\Leftrightarrow\frac{-3}{2}< x< 2\)

a) 3x^3 -10x+3 =(3x-1)(x-3)
| x | -vc | 1/3 | 5/4 | 3 | +vc | |||||||||
| 3x-1 | - | 0 | + | + | + | + | + | |||||||
| x-3 | - | - | - | - | - | 0 | + | |||||||
| 4x-5 | - | - | - | 0 | + | + | + | |||||||
| VT | - | 0 | + | 0 | - | 0 | + |
Kết luận
VT< 0 {dấu "-"} khi x <1/3 hoắc 5/4<x<3
VT>0 {dấu "+"} khi x 1/3<5/4 hoặc x> 3
VT=0 {không có dấu} khi x={1/3;5/4;3}

Dưới lớp 10 ko có cách nào để giải dạng này (hoặc nếu sử dụng chia trường hợp để giải thì sẽ mất vài trang giấy, không ai làm thế hết)

Tham khảo:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
\(a = - 3 < 0\), \(\Delta = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)
Bảng xét dấu:

b) \(f\left( x \right) = {x^2} - x - 12\)
\(a = 1 > 0\), \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = - 3,x = 4\)
Bảng xét dấu:

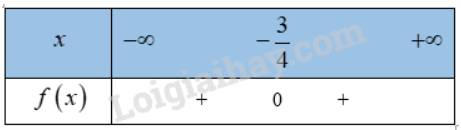
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)
=> \(f\left( x \right)\) có nghiệm duy nhất \(x = - \frac{3}{4}\)
Bảng xét dấu:
\(\left(x+1\right)\left(x-3\right)< 2\sqrt{x^2-2x-3}+3\)
\(\Leftrightarrow x\left(x+1\right)-3\left(x+1\right)< 2\sqrt{x^2-2x-3}+3\)
\(\Leftrightarrow x^2+x-3x-3< 2\sqrt{x^2-2x-3}+3\)
\(\Leftrightarrow x^2-2x-3< 2\sqrt{x^2-2x-3}+3\) (1)
Đặt \(t=\sqrt{x^2-2x-3}\) ( điều kiện \(t\ge0\) )
\(\Rightarrow bpt\left(1\right)\Leftrightarrow t^2< 2t+3\)
\(\Leftrightarrow t^2-2t-3< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}t< -1\left(loại\right)\\t>3\left(nhận\right)\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{x^2-2x-3}>3\)
\(\Leftrightarrow x^2-2x-3>9\)
\(\Leftrightarrow x^2-2x-12>0\)
\(\Leftrightarrow x\in\left(-\infty;1-\sqrt{13}\right)\cup\left(1+\sqrt{13};+\infty\right)\)
Vậy nghiệm của bất phương trình \(x\in\left(-\infty;1-\sqrt{13}\right)\cup\left(1+\sqrt{13};+\infty\right)\)