Cho hàm số: y=f(x)=x2-8
Tìm x biết y=17
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Dựa vào đồ thị hàm số ta thấy f ' ( x ) < 0 ⇔ x < − 6 − 1 < x < 2
( f ( 3 − x 2 ) ) ' = ( 3 − x 2 ) ' . f ' ( 3 − x 2 ) = − 2 x . f ' ( 3 − x 2 ) ⇒ ( f ( 3 − x 2 ) ) ' > 0 ⇔ x < − 6 − 1 < x < 0

Đáp án C
Xét hàm số ![]() . Khi đó hàm số
. Khi đó hàm số ![]() liên tục trên các đoạn
liên tục trên các đoạn ![]() ,
, ![]() và có
và có ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() .
.
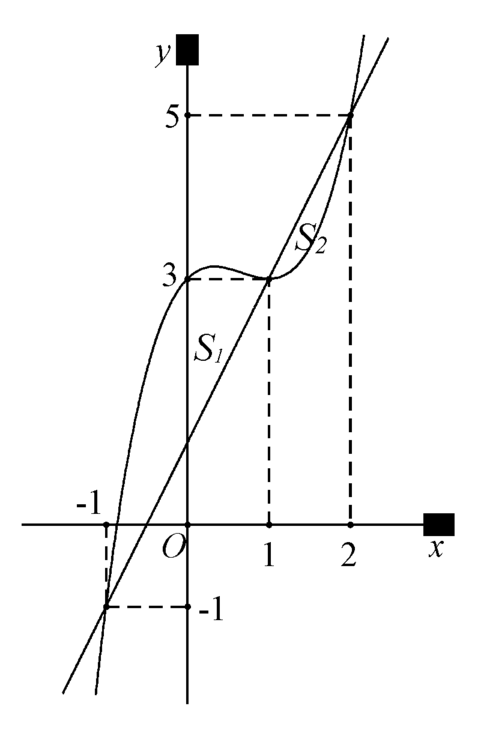
Do đó diện tích hình phẳng giới hạn bởi 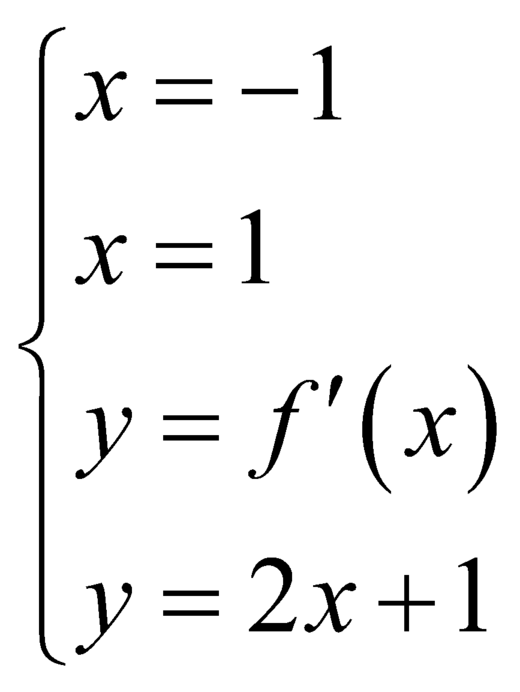 là
là
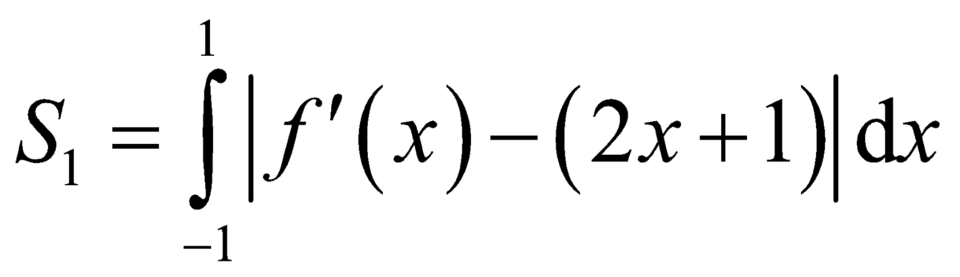
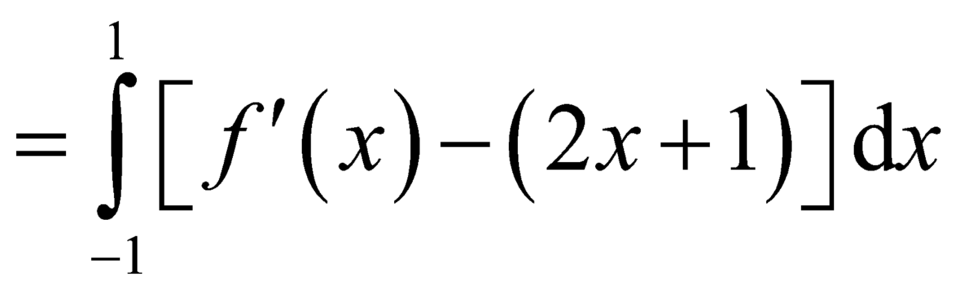
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.
Diện tích hình phẳng giới hạn bởi 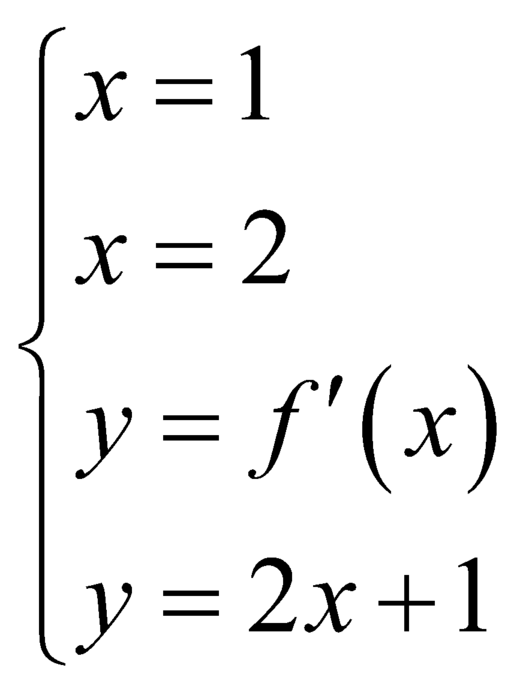 là
là
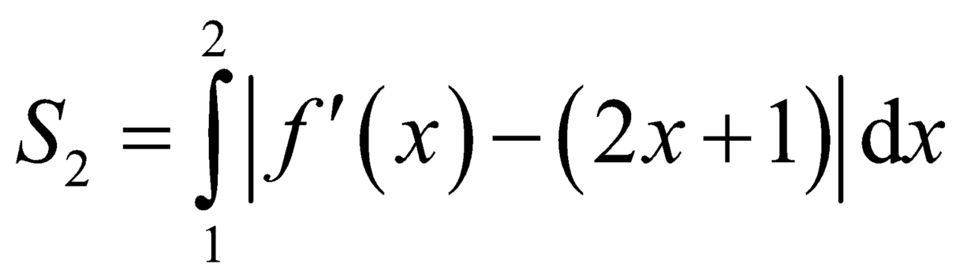
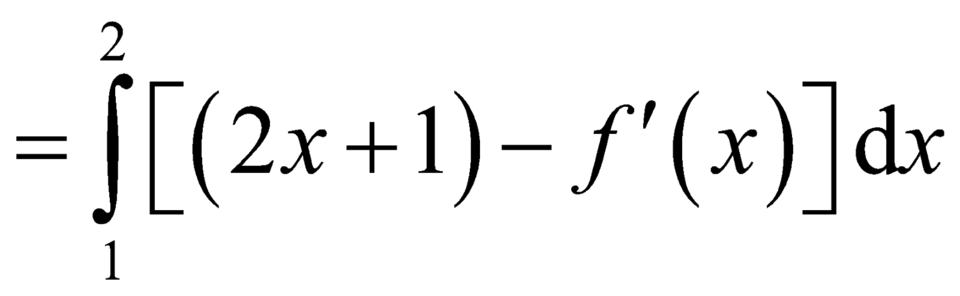
![]()
![]() .
.
Vì ![]() nên
nên ![]() .
.
\(y=f\left(x\right)=x^2-8\)
Thay \(y=17\) ta có:
\(17=x^2-8\)
\(\Rightarrow x^2=25\)
\(\Rightarrow x=5\) hoặc \(x=-5\)
Vậy \(x\in\left\{5;-5\right\}\)
Có hàm số y = f(x) = x2 - 8. Với y = 17
=> x2 - 8 = 17
x2 = 17 + 8
x2 = 25
=> x2 = 52
=> x = 5
Vậy với đồ thị hàm số y = f(x) = x2 - 8 và y = 17 thì ta có x = 5