Tính diện tích của tam giác cân biết đấy bằng 6cm và cạnh bên bằng 5cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


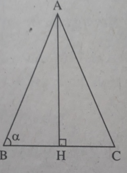
Xét tam giác cân ABC có AB = AC, ∠ (ABC) = α , đường cao AH (h.bs.13)


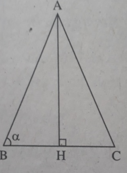
Xét tam giác cân ABC có AB = AC, ∠(ABC) = α , đường cao AH (h.bs.13)
AB = AC = b thì AH = bsin α , BH = bcos α nên diện tích tam giác ABC là
S = 1/2.AH.BC = AH.BH = b 2 sin α .cos α

Gọi độ dài 2 cạnh tam giác l lượt là x, y (đk)
AD Pi- ta-go ta có : x^2+y^2=5^2=25 (1)
Mà diện tích tam giác = 6 (cm2) => x*y/2=6 => x*y=12 (2)ư
Từ (1), (2) ta có hpt
Giải hpt => x=3, y=4 hoạc x=4, y=3
Kl ...

a:ΔSBC cân tại S có SM là trung tuyến
nên SM vuông góc BC
BC=6cm
=>BM=CM=3cm
SM=căn 5^2-3^2=4cm
Sxq=5*3/2*4=5*3*2=30cm2
Stp=30+5^2*căn 3/2=(60+25căn 3)/2cm2
b: BC vuông góc SM
BC vuông góc AM
=>BC vuông góc (SAM)

Câu 1:
Diện tích tam giác đều cạnh 3cm là:
\(S=\dfrac{3^2\cdot\sqrt{3}}{4}=\dfrac{9\sqrt{3}}{4}\left(cm^2\right)\)
Câu 2:
Nửa chu vi tam giác là:
\(P=\dfrac{C}{2}=\dfrac{8+8+6}{2}=\dfrac{22}{2}=11\left(cm\right)\)
Diện tích tam giác là:
\(S=\sqrt{P\cdot\left(P-A\right)\cdot\left(P-B\right)\cdot\left(P-C\right)}=\sqrt{11\cdot\left(11-8\right)^2\cdot\left(11-6\right)}\)
\(=\sqrt{11\cdot5\cdot9}=3\sqrt{55}\left(cm^2\right)\)

Gọi tam giác cần tìm là ABC cân tại A. Từ A kẻ AH vuông góc với BC.
=> BH=CH=\(\frac{6}{2}\)=3 (cm). theo định lí Py-ta-go => AH= 4cm
Vậy SABC= AH.BC.\(\frac{1}{2}\) = 4.6.\(\frac{1}{2}\)= 12 cm2
Bạn tự vẽ hình nhé
Từ A kẻ \(AH\perp BC\)
Xét \(\Delta ABC\) cân tại A có AH là đường cao (vì \(AH\perp BC\) )
=> AH đồng thời là đường trung tuyến
=> H là trung điểm của BC
=> BH = HC = \(\frac{6}{2}=3\left(cm\right)\)
Xét \(\Delta ABH\) vuông tại H có \(AH^2+BH^2=AB^2\) (định lí Py-ta-go)
<=> \(AH^2+3^2=5^2\)
<=> \(AH^2=25-9\)
<=> \(AH=4\) (vì \(AH\ge0\) )
Có \(S_{ABC}=\frac{1}{2}.6.4=12\left(cm^2\right)\)
Vậy diện tích của tam giác cân có đáy bằng 6cm và cạnh bên bằng 5cm là \(12cm^2\)
Chúc bạn học tốt :))