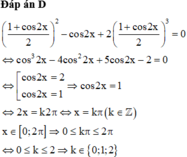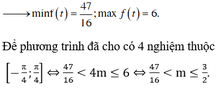tìm m để phương trình : sin6x+cos6x+2cos3xcosx−cos4x+m=0 có nghiệm thuộc đoạn...
Đọc tiếp
tìm m để phương trình : sin6x+cos6x+2cos3xcosx−cos4x+m=0 có nghiệm thuộc đoạn [\(\frac{\pi}{4}\);\(\frac{\pi}{2}\)]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 11 2018
(1) trở thành 4t2 – 2t -6 – m = 0 (2); △ ' = 25 + 4 m .
Để (1) vô nghiệm, ta sẽ tìm m sao cho (1) có nghiệm rồi sau đó phủ định lại.
(1) có nghiệm thì (2) phải có nghiệm thoả t o ∈ - 1 ; 1
Nếu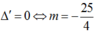 
, (2) có nghiệm kép 
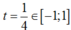nên 
thoả (1) có nghiệm.
Nếu 
, khi đó (2) phải có hai nghiệm phân biệt thoả 
8 tháng 10 2021
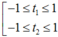
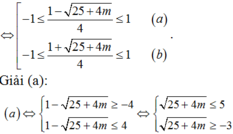
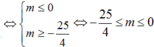
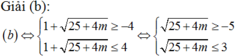
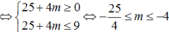
sin6x + cos6x = mcos24x
⇔ (sin2x + cos2x)3 - 3sin2x.cos2x . (sin2x + cos2x) = m.cos24x
⇔ 1 - 3sin2x.cos2x = m.cos24x
⇔ 8 - 6.(2sinx.cosx)2 = 8m.cos24x (nhân cả 2 vế vs 8)
⇔ 8mcos24x + 6sin22x - 8 = 0
⇔ 8mcos24x - 3cos4x - 11 = 0
Đặt t = cos4x. Cần tìm m để phương trình 8mt2 - 3t - 11 = 0 có nghiệm t ∈ [- 1 ; 1]
28 tháng 10 2022
cos 6x+cos4x=sin7x-sin3x
=>2*cos5x*cosx=2*cos5x*sin2x
=>cos5x(cosx-sin2x)=0
=>cos5x=0 hoặc sin2x=sin(pi/2-x)
=>5x=pi/2+kpi hoặc 2x=pi/2-x+k2pi hoặc 2x=pi/2+x+k2pi
=>x=pi/10+kpi/5; x=pi/6+k2pi/3; x=pi/2+k2pi
