aaa
+
1
=bccc
Thay các chữ cái sau bằng số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DK
11 tháng 4 2019
Đáp án : C
Các phép lai cho ra đời con có 6 loại kiểu gen là : (2) (3) (4)
Phép lai 1 : Cái Aa x đực Aaa = ( A: a) ( A: a) => 3 kiểu gen
Phép lai 2 : Cái Aaa x đực AAa = (Aa,aa, A: a) ( A: a) => 6 kiểu gen
Phép lai 3 : Cái Aaa x đực Aaa = (Aa,aa, A: a) ( A: a) => 6 kiểu gen
Phép lai 4 Cái AAa x đực Aa = (AA : Aa :A : a) ( A: a) => 6 kiểu gen
Phép lai 5 cho 3 kiểu gen
27 tháng 10 2021
Câu đầu có thể là: a=1 và b=4; a=2 và b=3; a=3 và b=2; a=4 và b=1.
TN
1
24 tháng 11 2017
Ta có:
\(1+2+3+....+n=\overline{aaa}\)
\(\Rightarrow\left(n+1\right).n\div2=\overline{aaa}\)
\(\Rightarrow\left(n+1\right).n\div2=111.a\)
\(\Rightarrow\left(n+1\right).n=111.a.2\)
\(\Rightarrow\left(n+1\right).n=37.6a\)
Vì 37 là số nguyên tố \(\Rightarrow n+1⋮37\) hoặc \(n⋮37\)
Mà \(\overline{aaa}\le999\Rightarrow n< 50\)
\(\Rightarrow n+1=37\)hoặc \(n=37\)
Nếu \(n=37\Rightarrow6a=38\) (loại)
Nếu \(n+1=37\Rightarrow n=36\Rightarrow a=36\)
Thử lại: \(\left(36.37\right)\div2=666\) (thỏa mãn)
Vậy \(n=36;a=6\)
CM
19 tháng 5 2017
- Vì A≠G mà chữ số hàng chục của tổng là 0 nên phép cộng có nhớ 1 sang hàng trăm nên ở hàng trăm: H + N + 1 (nhớ) = 10; nhớ 1 sang hàng nghìn. Do đó H + N = 10 - 1 = 9.
- Phép cộng ở hàng nghìn: N + 1 (nhớ) = 2 nên N = 2 - 1 = 1.
Thay N = 1 ta có: H + 1 = 9 nên H = 9 - 1 = 8
- Phép cộng ở hàng đơn vị: Có 2 trường hợp xảy ra:
* Trường hợp 1: Phép cộng ở hàng đơn vị không nhớ sang hàng chục.
Khi đó: M + O = 0 và A + G = 10.
Ta có bảng: (Lưu ý 4 chữ M, O, A, G phải khác nhau và khác 1; 8)
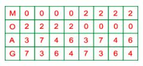
* Trường hợp 2: Phép cộng ở hàng đơn vị có nhớ 1 sang hàng chục.
Khi đó: M + O = 12 và A + G = 9. Ta có bảng:
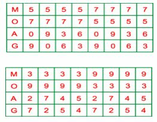
Vậy bài toán có 24 đáp số như trên.
XS
2
22 tháng 9 2016
a .a tận cùng a suy ra a thuộc {0;1;5;6}
dễ thấy a ko = 0 , a ko = 1
Thử
555 x 5 =2775 loại
666x6=3996 đúng
a=9
b=1
c=0
999+1=1000
a=9
b=1
c=0