cho tam giác ABC VUÔNG Tại A . gọi I là trung điểm của bc . trên tia đối của IA lấy điểm D sao chi ID=Ia
a) chứng minh rằng tam giá BID = tam giác CIA
b) CMR BD vuông góc AB
c) qua a kẻ đường song song với BC cắt đường thẳng BD tại M. chứng minh. tam giác BAM= tam giác ABC
d) chứng minh rằng AB là phân giác của góc DAM

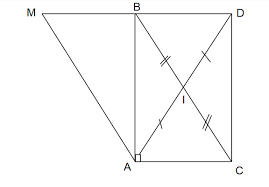
Mình vẽ nhầm hình nha, để mình vẽ lại ở dưới cái nào để chữ vẽ lại thì bạn vẽ cái đó
Đây là bài làm
a) Δ BID và Δ CIA có:
ID=IB (gt)
DIB=CIA (đói đỉnh)
IA=ID (gt)
=> Δ BID=Δ CIA (c.g.c)
b) Ta có: AM // BC
=> MAB=CAB (so le trong)
Δ BID=Δ CIA (cmt)
=> BDI=CAI ( 2 góc tương ứng)
và chúng ở vị trí so le trong
=> CA // DM
Ta có: CA // DM (cmt)
=> CAB=MBA=900 (so le trong)
Δ BAM và Δ ABC có:
MAB=CAB (cmt)
BA cạnh chung
CAB=MBA=900 (cmt)
=> Δ BAM=Δ ABC (g.c.g)
c)Δ BAM=Δ ABC
=> BM=AC (2 cạnh tương ứng)
Mà AC=BD ( Δ BID=Δ CIA)
=>BM=BD
MBA=900 (cmt)
mà MBA+ABD=1800 ( kề bù)
900 +ABD=1800
=>ABD=1800-900=900
=>MBA=ABD
Δ ADB=Δ AMB có:
BM=BD (cmt)
MBA=ABD (cmt)
AB cạnh chung
=> Δ ADB=Δ AMB ( g.c.g)
=>MAB=DAB (2 góc tương ứng)
Vậy AB là phân giác góc DAM
@Trần Nghiên Hy mk đang quen cách làm của lớp 8 rồi, chả nhớ j lớp 7 cả