Tính tổng S = 1/2+1/4+1/8+.......+1/256+1/512
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: A =1/2+1/4+1/8+1/16+....+1/256+1/512
=> 2A = 1 + 1/2 + 1/4 + 1/8 + ...+ 1/128 + 1/256
=> 2A - A = (1 + 1/2 + 1/4 + 1/8 + ...+ 1/128 + 1/256 -(1/2+1/4+1/8+1/16+....+1/256+1/512 )
A = 1 - 1/512 = 511/512

1/2 + 1/4 + 1/8 + 1/16 + ... + 1/256 + 1/512
= 256/512 + 128/512 + 64/512 + ... + 2/512 + 1/512
= 256 + 128 + 64 + .. + 2 + 1 / 512
= ???????
s=1/2+1/4+1/8+1/16+.....+1/256+1/512
sx2=(1/2+1/4+1/8+1/16+....+1/256+1/512)x2
sx2=1+1/2+1/4+1/8+......+1/126+1/256
sx2-s=(1+1/2+1/4+1/8+......+1/256)-(1/2+1/4+1/8+1/16++.....+1/256+1/512)
1+1/2+1/4+1/8+......+1/256-1/2-1/4-1/8-1/16-.....1/256-1/512
=1-1/512=511/512

Vậy dãy số đó là:
1/2 + 1/4 + 1/8 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 =
256/512 + 128/512 + 64/512 + 32/512 + 16/512 + 8/512 + 4/512 + 2/512 + 1/512 511/512
Đáp số: 511/512

Đặt \(A=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{256}+\dfrac{1}{512}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{128}+\dfrac{1}{256}\)
\(\Rightarrow A=2A-A=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{128}+\dfrac{1}{256}-\dfrac{1}{2}-\dfrac{1}{4}-\dfrac{1}{8}-...-\dfrac{1}{256}-\dfrac{1}{512}\)
\(\Rightarrow A=1-\dfrac{1}{512}=\dfrac{511}{512}\)

A=1/2+1/4+1/8.....+1/256+1/512
2A=1+1/2+1/4+1/8...1/256
A=(1+1/2+1/4+1/8...1/256)-(1/2+1/4+1/8.....+1/256+1/512)
A=1-1/512
A=511/512
511/512
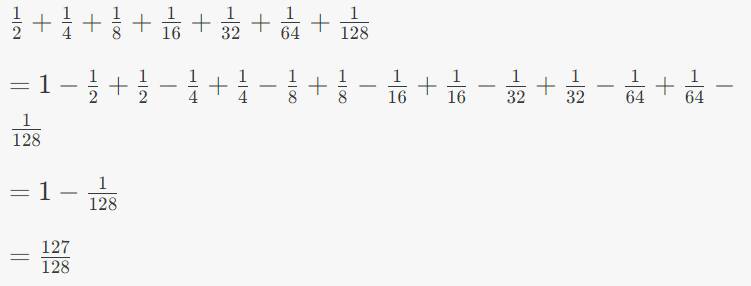
1/2 + 1/4+ 1/8+ 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512
= 1 – 1/2 + 1/2- 1/4 + 1/4 – 1/8 + 1/8 – 1/16 + 1/16 – 1/32 + 1/32 – 1/64 + 1/64 – 1/128 + 1/128 – 1/256 – 1/256 – 1/512
= 1 – 1/512
= 511/512 .
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + 1/1024
Ta có :
1/512 = 1×2 / 512×2 = 2/1024
1/256 = 1×4 / 256×4 = 4/1024
1/128 = 1×8 / 128×8 = 8/1024
1/64 = 1×16 / 64×16 = 16/1024
1/32 = 1×32 / 32×32 = 32/1024
1/16 = 1×64 / 16×64 = 64/1024
1/8 = 1×128 / 8×128 = 128/1024
1/4 = 1×256 / 4×256 = 256/1024
1/2 = 1×512 / 2×512 = 512/1024
___________________________
=>
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512 + 1/1024
= 512/1024 + 256/1024 + 128/1024 + 64/1024 + 32/1024 + 16/1024 + 8/1024 + 4/1024 + 2/1024 + 1/1024
= (512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1) / 1024
= 1023/1024