Giải dùm mình
1/ Cho tam giác nhọn ABC nội tiếp đường tròn(O). Gọi H là trực tâm của tam giác đó, AK là đường kính của đường tròn(O)
a/ C/m: Tứ giác BHCK là hình bình hành
b/ Gọi M là trung điểm của BC. C/m: OM=\(\frac{AH}{2}\)
Thank!!![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔABK nội tiếp đường tròn
AK là đường kính
Do đó: ΔABK vuông tại B
Xét (O) có
ΔACK nội tiếp đường tròn
AK là đường kính
Do đó: ΔACK vuông tại C
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành

\(a,\widehat{ABK}=\widehat{ACK}=90^0\) (góc nt chắn nửa đường tròn) nên \(\Delta ABK;\Delta ACK\) vuông tại B và C
\(b,\left\{{}\begin{matrix}CK//BH\left(\perp AC\right)\\BK//CH\left(\perp AB\right)\end{matrix}\right.\Rightarrow BHCK\) là hbh
\(c,\left\{{}\begin{matrix}AO=OM=R\\OM//AH\left(\perp BC\right)\end{matrix}\right.\Rightarrow HM=MK\)
Hình bình hành BHCK có M là trung điểm HK nên cũng là trung điểm BC
\(d,\left\{{}\begin{matrix}AO=OK=R\\HM=MK\left(cm.trên\right)\end{matrix}\right.\Rightarrow OM\) là đtb tam giác AHK
\(\Rightarrow OM=\dfrac{1}{2}AH\)

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD vuông góc AB
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC vuông góc CD
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔHDA có
I,O lần lượt là trung điểm của DH,DA
=>IO là đường trung bình
=>IO//AH và IO=AH/2
=>AH=2IO

a: Xét tứ giác BHCD có
M là trung điểm của BC
M là trung điểm của HD
Do đó: BHCD là hình bình hành

a) Ta có: \(\angle BEC=\angle BDC=90\Rightarrow BCDE\) nội tiếp
Gọi I là trung điểm BC
Vì \(\Delta BEC\) vuông tại E có I là trung điểm BC \(\Rightarrow IE=IB=IC\)
Vì \(\Delta BDC\) vuông tại D có I là trung điểm BC \(\Rightarrow ID=IB=IC\)
\(\Rightarrow ID=IE=IB=IC\Rightarrow I\) là tâm của (BCDE)
b) Vì AK là đường kính \(\Rightarrow\angle ABK=\angle ACK=90\)
\(\Rightarrow\left\{{}\begin{matrix}BK\bot AB\\CK\bot AC\end{matrix}\right.\) mà \(\left\{{}\begin{matrix}CH\bot AB\\BH\bot AC\end{matrix}\right.\Rightarrow\) \(CH\parallel BK,BH\parallel CK\)
\(\Rightarrow BHCK\) là hình bình hành có I là trung điểm BC
\(\Rightarrow H,I,K\) thẳng hàng

a) Xét tứ giác AEHF có
\(\widehat{AFH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{AFH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI
c: G là trọng tâm
nên AG=2AI
Xét ΔAHD có
AI là trung tuyến
AG=2/3AI
DO đó: G là trọng tâm

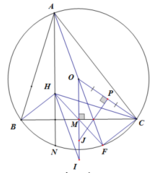
b) Vì AHIO là hình bình hành nên OI = AH = 2OM
Gọi P là trung điểm OC ⇒ PJ là trung trực OC ⇒ PJ ⊥ OC.
Có OM là trung trực BC ⇒ OM ⊥ BC. Suy ra
Δ O J P ~ Δ O C M ( g . g ) ⇒ O J O C = O P O M ⇒ O J . O M = O C . O P ⇒ O J .2 O M = O C .2 O P ⇒ O J . O I = O C . O C = R 2