giá trị của b để y=x+b và y=x2-3x+5 có đúng một điểm chung
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Bảng giá trị
x |
-2 |
-1 |
0 |
1 |
2 |
y = –x2 |
-4 |
-1 |
0 |
-1 |
-4 |
Đồ thị:
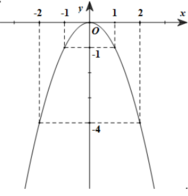
b) Xét phương trình hoành độ giao điểm của (d) và (P): –x2 = 4x – m ⇔ x2 + 4x – m = 0 (1)
(d) và (P) có đúng 1 điểm chung ⇔ phương trình (1) có nghiệm kép ⇔ ∆’ = 22 – (–m) = 0
ó 4 + m = 0 ⇔ m = –4
Vậy m = –4

Phương trình hoành độ giao điểm - x 2 - 2 x + 3 = x 2 - m
⇔ 2 x 2 + 2 x - m - 3 = 0 *
Để hai đồ thị hàm số có điểm chung khi và chỉ khi phương trình (∗) có nghiệm
⇔ ∆ = 1 - 2 - m - 3 ≥ 0 ⇔ m ≥ - 7 2
Đáp án cần chọn là: D

Ta có phương trình hoành độ giao điểm
m x + 4 = 2 x + 3 x + 1 ⇒ m x 2 - m + 2 x + 1 = 0
Phương trình có hai nghiệm phân biệt
⇔ m ≠ 0 ∆ = m + 2 2 - 4 m > 0 m - m + 2 + 1 ≠ 0 ⇔ m ≠ 0
Chọn đáp án C

Chọn đáp án D
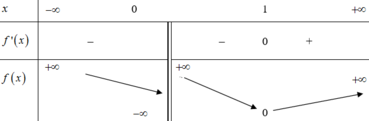
Phương pháp
Đồ thị hàm số y=f(x) và đường thẳng y=g(x) có duy nhất 1 điểm chung ⇒ phương trình hoành độ giao điểm f(x)=g(x) có nghiệm duy nhất.
Cách giải
Phương trình hoành độ giao điểm của đồ thị hai đồ thị hàm số là
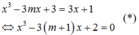
Hai đồ thị hàm số có duy nhất 1 điểm chung khi và chỉ khi phương trình (*) có nghiệm duy nhất




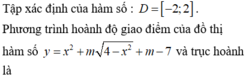
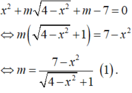
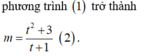

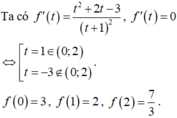

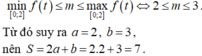



Phương trình hoành độ giao điểm là:
\(x^2-3x+5=x+b\)
\(\Leftrightarrow x^2-4x+5-b=0\)
Để hai đồ thị có đúng một điểm chung thì \(16-4\left(5-b\right)=0\)
=>4(5-b)=16
=>5-b=4
hay b=1