Giúp mình câu 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
4 tháng 10 2020
\(\frac{75.5^4+175.5^4}{20.25.125-625.75}=\frac{\left(75+175\right).5^4}{4.5.25.5^3-5^4.75}\)
\(=\frac{250.5^4}{100.5^4-5^4.75}=\frac{250.5^4}{\left(100-75\right).5^4}\)
\(=\frac{250}{25}=10\)
giúp mình câu 3; câu 4 với mình cần gấp
HV
3
10 tháng 9 2023
3d:
20<x<45
x chia 4 dư 1 nên x-1 thuộc B(4)
=>\(x-1\in\left\{0;4;...;44;48\right\}\)
=>\(x\in\left\{1;5;...;45;49\right\}\)
mà 20<x<45
nên x thuộc {21;26;31;35;41}
4:
a: A={x∈N|51<=x<=127}
b: B={x∈N|100<=x<=999}
c: C={x∈N|x=7k+5; 0<=k<=8}
GB
1
29 tháng 10 2021
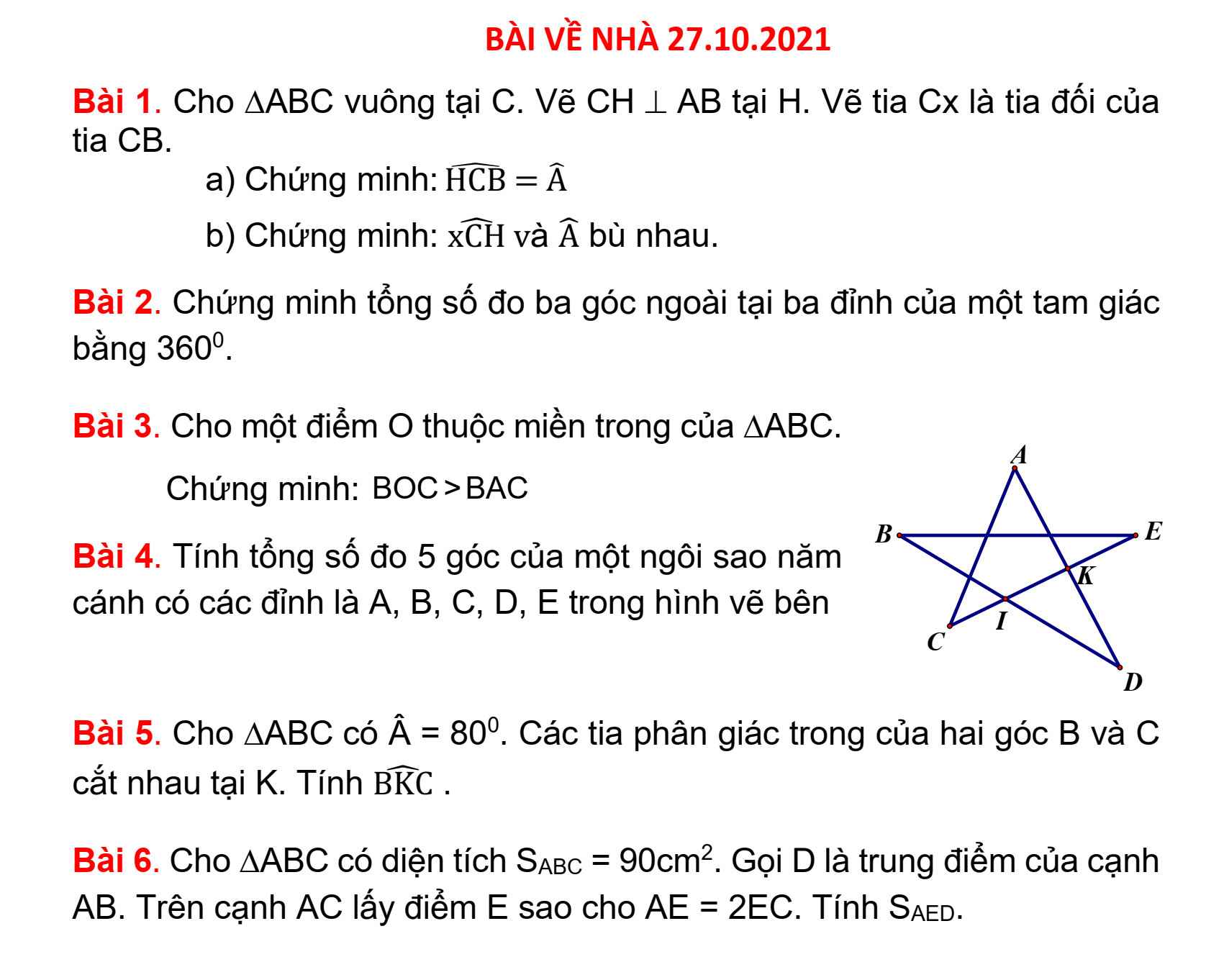
Bài 5:
\(\widehat{BKC}=180^0-\left(\widehat{KBC}+\widehat{KCB}\right)\)
\(=180^0-\dfrac{180^0-80^0}{2}\)
\(=180^0-50^0=130^0\)
DN
giúp mình câu 4 câu 6
0
NA
,
3
6 tháng 11 2021
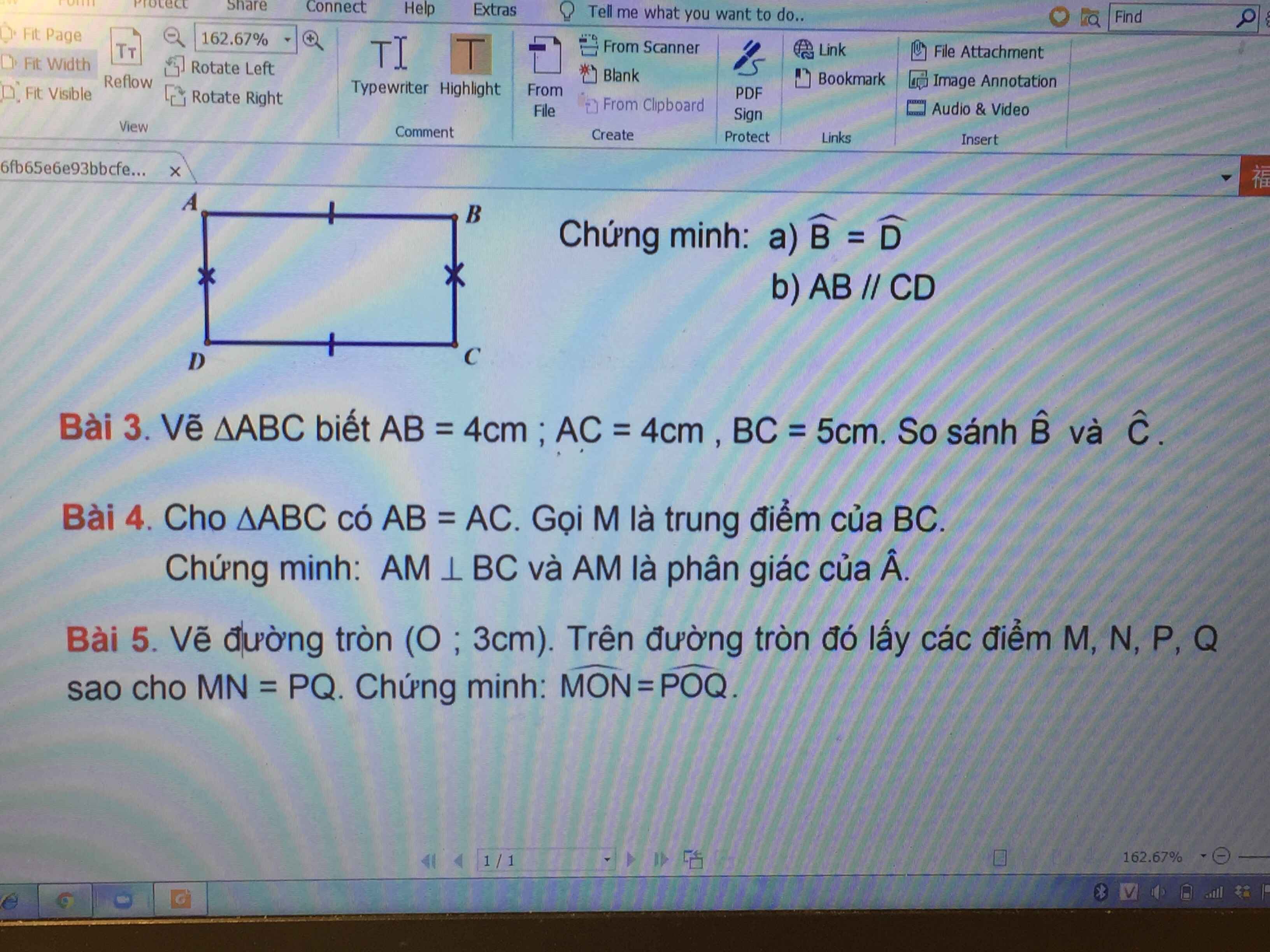
Bài 4:
Vì \(\left\{{}\begin{matrix}AB=AC\\BM=MC\\AM.chung\end{matrix}\right.\) nên \(\Delta AMB=\Delta AMC\left(c.c.c\right)\)
Do đó \(\left\{{}\begin{matrix}\widehat{AMB}=\widehat{AMC}\\\widehat{MAB}=\widehat{MAC}\end{matrix}\right.\)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\) nên \(\widehat{AMB}=\widehat{AMC}=90^0\) hay AM⊥BC
\(\widehat{MAB}=\widehat{MAC}\) (cm trên) nên AM là pg góc BAC
HP
14 tháng 9 2021
1.
ĐK: \(x\ge0;x\ne9\)
\(Q=-\dfrac{1}{\sqrt{x}-3}\in Z\)
\(\Leftrightarrow\sqrt{x}-3\inƯ_1=\left\{\pm1;\pm3\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;4;6\right\}\)
\(\Leftrightarrow x\in\left\{0;4;16;36\right\}\)
HP
14 tháng 9 2021
2.
ĐK: \(x\ge0;x\ne1\)
\(Q=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}\in Z\)
\(\Leftrightarrow1-\dfrac{2}{\sqrt{x}-1}\in Z\)
\(\Leftrightarrow\sqrt{x}-1\inƯ_2=\left\{\pm1;\pm2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
\(\Leftrightarrow x\in\left\{0;4;9\right\}\)
PN
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
0
đề như thế nào vậy bạn