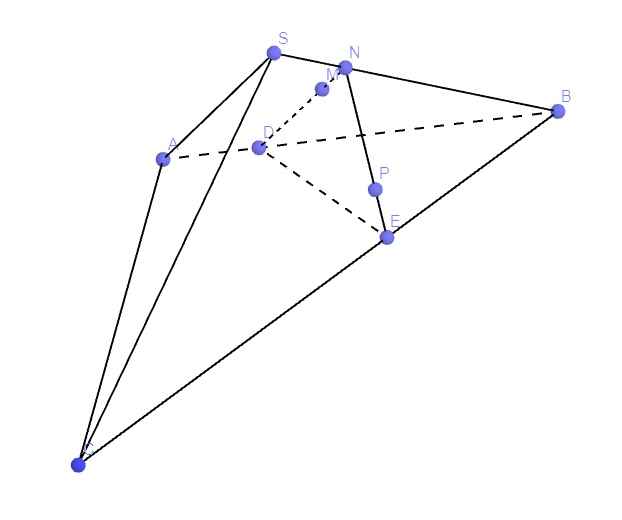
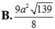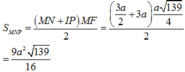Cho hình chóp SABC. Gọi M , N là các điểm trên SA , SB , P là điểm trong mf SBC. Tìm thiết diện tạo bởi (MNP) và hình chóp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


À, "không tính" là đang nói tới D, E trong hình vẽ của em (nằm trên cạnh chóp kéo dài), không phải D, E trong hình của mình (nằm trên cạnh chóp)


Coi như vị trí các điểm không có gì đặc biệt
Trong mặt phẳng \(SAB\)nối \(MN\)cắt \(AB\) kéo dài tại \(E\)
Trong mặt phẳng \(ABCD\)nối \(EP\)kéo dài lần lượt cắt \(BC\)tại \(F\), \(AD\)tại \(G\)
=> Tứ giác \(MNFG\)là thiết diện của \(MNP\)và chóp

Coi như vị trí các điểm không có gì đặc biệt
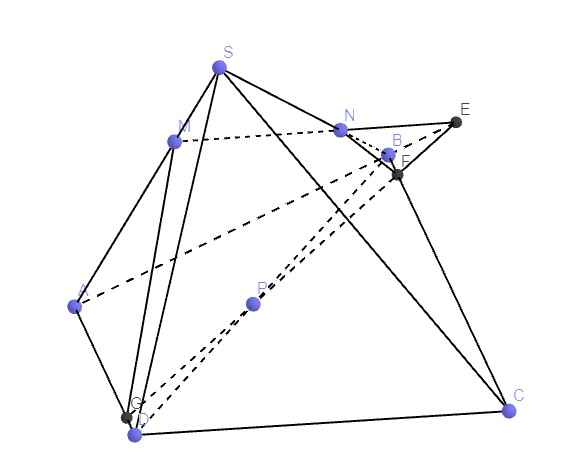
Trong mp (SAB), nối MN cắt AB kéo dài tại E
Trong mp (ABCD), nối EP kéo dài lần lượt cắt BC tại F và AD tại G
\(\Rightarrow\) Tứ giác MNFG là thiết diện của (MNP) và chóp

Lời giải:
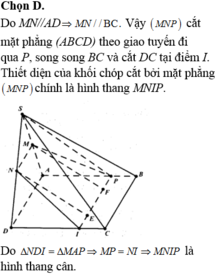
Gọi $Q$ là điểm nằm trên $DC$ sao cho $AD\parallel PQ$
Khi đó: $MN\parallel AD\parallel PQ$ nên $Q\in (MNP)$
$(MNPQ)$ chính là thiết diện của hình chóp cắt bởi $(MNP)$
Giờ ta cần tìm diện tích hình thang $MNPQ$
$SA=SD; DB=SC; AB=CD$ nên $\triangle SAB=\triangle SDC$
Tương ứng ta có $MP=NQ$
$MN=\frac{AD}{2}=\frac{3a}{2}$
$PQ=AD=3a$
$\Rightarrow MNPQ$ là hình thang cân.
Áp dụng định lý cos:
$\cos \widehat{SAB}=\frac{SA^2+AB^2-SB^2}{2SA.AB}=\frac{MA^2+AP^2-MP^2}{2MA.AP}$
$\Leftrightarrow \frac{9a^2+9a^2-27a^2}{2.3a.3a}=\frac{\frac{9}{4}a^2+4a^2-MP^2}{2.\frac{3}{2}a.2a}$
$\Rightarrow MP^2=\frac{37}{4}a^2$
$\Rightarrow h_{MNPQ}=\sqrt{MP^2-(\frac{PQ-MN}{2})^2}=\frac{\sqrt{139}}{4}a$
Diện tích thiết diện:
$S=\frac{MN+PQ}{2}.h=\frac{9\sqrt{139}}{16}a^2$

Câu 1: bạn xem lại đề, chóp S.ABC nhưng lại có SD?
Câu 2: giống câu 1, vẫn là chóp S.ABC và yêu cầu tìm giao điểm liên quan đến điểm D ko tồn tại?