Cho biết chu vi của một tam giác lad 56,4 cm và các chiều cao tỉ lệ với 1/3 ; 0.25 ; 0.2 . Tính độ dài mỗi cạnh của mỗi tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài mỗi cạnh tam giác là a,b,c(a,b,c>0)
Theo bài ra ta có:\(\left\{{}\begin{matrix}a+b+c=56,4\\\dfrac{a}{\dfrac{1}{\dfrac{1}{3}}}=\dfrac{b}{\dfrac{1}{0,25}}=\dfrac{c}{\dfrac{1}{0,2}}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a+b+c=56,4\\\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\end{matrix}\right.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{56,4}{12}=4,7\)
\(\dfrac{a}{3}=4,7\Rightarrow a=14,1\\ \dfrac{b}{4}=4,7\Rightarrow b=18,8\\ \dfrac{c}{5}=4,7\Rightarrow c=23,5\)
Vậy ...

lại bắt đầu nè tìm đường cao như bình thường rồi xét đường cao = cạnh => đó là các cạnh bla bla
Gọi chiều cao của tam giác lần lượt là a, b, c
các cạnh của tam giác lần lượt là x, y, z
Ta có: \(\frac{a}{3}=\frac{b}{5}=\frac{c}{6}\)
Đặt \(\frac{a}{3}=\frac{b}{5}=\frac{c}{6}=k\left(k\ne0\right)\)\(\Rightarrow a=3k\), \(b=5k\), \(c=6k\)
\(S_{\Delta}=\frac{1}{2}ax=\frac{1}{2}by=\frac{1}{2}cz\)\(\Rightarrow ax=by=cz\)
\(\Rightarrow3k.x=5k.y=6k.z\)\(\Rightarrow3x=5y=6z\)\(\Rightarrow\frac{3x}{30}=\frac{5y}{30}=\frac{6z}{30}=\frac{x}{10}=\frac{y}{6}=\frac{z}{5}=\frac{x+y+z}{10+6+5}=\frac{42}{21}=2\)
\(\Rightarrow x=2.10=20\), \(y=2.6=12\), \(z=2.5=10\)
Vậy độ dài 3 cạnh của tam giác lần lượt là 20 cm, 12 cm, 10 cm

Answer:
Ta gọi chiều cao của ba cạnh là: x, y, z (x, y, z > 0)
Vì chiều cao tỉ lệ nghịch với \(\frac{1}{3};\frac{1}{4};\frac{1}{5}\Rightarrow\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\) và \(x+y+z=70,5\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{70,5}{12}=\frac{47}{8}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{141}{8}\\y=\frac{47}{2}\\z=\frac{235}{8}\end{cases}}\)

Gọi x , y , z lần lượt là độ dài các cạnh của tam giác (cm) ( x , y , z > 0 )
Chu vi của tam giác là 36 cm nên x + y + z = 36
Vì các cạnh của tam giác tỉ lệ với các số 3 , 4 , 5 nên x/3 =y/4 = z/5
Theo tính chất dãy tỉ số bằng nhau ta có :
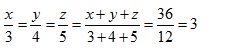
Suy ra : x = 3 . 3 = 9 (TM)
y = 4 . 3 = 12 (TM)
z = 5 . 3 = 15 (TM)
Vậy độ dài các cạnh của tam giác lần lượt là : 9cm , 12cm , 15cm .

Ta có hình vẽ:
A B C
Ta có sơ đồ:
Cạnh AB: |----------|
Cạnh BC: |----------|----------|
Cạnh CA: |----------|----------|----------|
Tổng số phần bằng nhau là:
1 + 2 + 3 = 6 ( phần )
Cạnh AB dài:
45 : 6 x 1 = 7, 5 ( cm )
Cạnh BC dài:
45 : 6 x 2 = 15 ( cm )
Cạnh CA dài:
45 : 6 x 3 = 22, 5 ( cm )
Đáp số: ...
~ Chúc bạn học tốt ~
Tổng số phần bằng nhau là :
2 + 3 + 4 = 9 ( phần )
Cạnh AB là :
45 : 9 x 2 = 10 ( cm )
Cạnh BC là :
45 : 9 x 3 = 15 ( cm )
Cạnh CA là :
45 : 9 x 4 = 20 ( cm )
Đ/S : ...............
Gọi độ dãi mỗi cạnh của tam giác là: a,b,c tỉ lệ với \(\frac{1}{3};0,25;0,2\) => \(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{5}}\)
Áp dụng t/c dãy tỉ số bằng nhau, ta có:
\(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{5}}=\frac{a+b+c}{\frac{1}{3}+\frac{1}{4}+\frac{1}{5}}=\frac{56,4}{\frac{47}{60}}=72\)
=> \(\begin{cases}a=24\\b=18\\c=\frac{72}{15}\end{cases}\)
nit mù tịt đầu óc hột vịt lộn, ng ta cho độ dài các đg cao.....