K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
4 tháng 10 2021
- Đặt tại các giao lộ, khúc cua: Gương cầu lồi dạng có đường kính lớn (D600 trở lên) thường được đặt ở các giao lộ, khúc cua hay đường đèo để giúp lái xe dễ dàng quan sát. Từ đó, điều chỉnh tốc độ cho phù hợp.
4 tháng 10 2021
MỌI NGƯỜI GIÚP EM VỚI Ạ EM ĐANG THẬT SỰ CẦN RẤT GẤP TẠI VÌ CÒN 1 TIẾNG NỮA PHẢI NỘP BÀI RỒI Ạ MÀ EM KHÔNG BIẾT LÀM MNG GIÚP EM VỚI CẢ 3 CÂU LUN Ạ!!!!
13 tháng 5 2021
tk
1. Mở bài
Giới thiệu vấn đề cần nghị luận: Phương pháp học đi đôi với hành. (Học sinh hình thành mở bài trực tiếp hoặc gián tiếp tùy vào khả năng của mình).
2. Thân bài
a. Giải thích
“Học đi đôi với hành”: lĩnh hội kiến thức trong sách vở, qua lời dạy của thầy cô, của người có kinh nghiệm, hiểu biết và áp dụng những lí thuyết đó vào thực tế cuộc sống để thực hiện công việc của mình và rút ra bài học cho bản thân tiến bộ hơn.
→ Lời khuyên nhủ con người không nên quá tập trung vào lí thuyết trên sách vở mà cần thực hành nhiều hơn nữa để rút ra kinh nghiệm.
b. Phân tích
Sách vở cung cấp cho chúng ta vô vàn kiến thức thuộc nhiều lĩnh vực khác nhau, chúng ta có thể tìm hiểu, học hỏi nhiều điều hay lẽ phải để mở mang tri thức, tầm hiểu biết của mình.
Việc thực hành, áp dụng những kiến thức sách vở vào cuộc sống giúp chúng ta rút ra những bài học thực tiễn để hoàn thiện công việc của mình và rút ngắn khoảng cách đến thành công.
Có học mà không có hành thì cũng chỉ là những kiến thức suông vì giữa học và hành có nhiều sự khác biệt. Có hành mà không được học sẽ không vỡ lẽ ra nhiều điều và sẽ chỉ dừng ở một mức độ nhất định. Vì vậy học hỏi và thực hành cần đi đôi với nhau để bổ sung cho nhau giúp con người hoàn thiện chặng đường chinh phục điều mình đang theo đuổi.
c. Chứng minh
Học sinh tự lấy dẫn chứng cho bài làm văn của mình.
Lưu ý: dẫn chứng phải xác thực, nổi bật được nhiều người biết đến.
d. Phản biện
Có nhiều bạn chỉ chăm chú vào học kiến thức trong sách vở, miệt mài với đèn sách nhưng không quan tâm đến việc áp dụng kiến thức đó vào thực tế. Lại có những người tuy có kinh nghiệm, được áp dụng thực tế nhưng lại không tích lũy, không có đủ kiến thức cần thiết. Những người này cần phải cố gắng khắc phục những thứ mình còn thiếu sót để hoàn thiện bản thân.
3. Kết bài
Khái quát lại vấn đề nghị luận (học đi đôi với hành) và liên hệ, rút ra bài học cho bản thân.
LH
Lê Huy Tường
VIP
13 tháng 5 2021
tk
Học tập là nhiệm vụ quan trọng hàng đầu của mỗi con người, nhưng đôi khi người ta quên hiểu rõ ràng và đầy đủ rằng, học tập không phải đơn thuần chỉ là lĩnh hội các tri thức mang tính lí thuyết mà còn là sự vận dụng, ứng dụng những lí thuyết vào thực tế. Đó là lí do vì sao chúng tôi muốn giải thích và làm rõ câu tục ngữ : “Học đi đôi với hành”.
Trước hết, “học” mà câu tục ngữ đề cập chính là việc tiếp nhận những kiến thức trên lớp, chính xác hơn thì đó là tiếp nhận lí thuyết. Còn “hành” chính là vận dụng, ứng dụng những lí thuyết vào thực tế cuộc sống. “Đi đôi” có nghĩa là luôn song hành với nhau, không thể nào tách rời. Toàn bộ câu tục ngữ có thể hiểu chính là, việc ta tiếp nhận kiến thức hay lí thuyết sẽ luôn phải đi cùng với việc ứng dụng, vận dụng những điều đó trong thực tế cuộc sống của chúng ta, như vậy mới có ý nghĩa.
Vậy tại sao “học” phải “đi đôi với hành”? Nếu con người chỉ “học” không “hành” hay chỉ “hành” không “học” thì có được không? Lí giải điều này sẽ giúp ta hiểu sâu sắc ý nghĩa câu tục ngữ. Nếu như “học” không “hành”, chúng ta có thể sẽ rất giỏi lí thuyết, thế nhưng kiến thức lí thuyết sâu rộng cũng sẽ trở nên vô ích khi nó không giúp gì cho cuộc sống con người trở nên tốt đẹp hơn. Vậy chúng ta sẽ “hành” để giúp ích cho cuộc sống, nhưng nên hiểu nếu “hành” mà không có lí thuyết chỉ đường, chúng ta biết bắt đầu từ đâu, biết “hành” như thế nào? “Hành” mà không “học”, con người chắc chắn sẽ thất bại. Tóm lại, “học đi đôi với hành” là một chân lí, học định hướng, giúp cho việc vận dụng có hiệu quả và ngược lại, việc vận dụng sẽ làm cho lí thuyết được học trở nên có ý nghĩa, đồng thời quay lại kiểm nghiệm tính đúng đắn của lí thuyết.
Chúng ta nhìn thấy rất nhiều người thành công là kết quả của việc vận dụng hợp lí và linh hoạt giữa lí thuyết và ứng dụng. Nhiều bạn trẻ có thể học không quá xuất chúng, nhưng ngoài học, các bạn còn hiểu tầm quan trong của ứng dụng nên tích cực học hỏi từ thực tế, trải nghiệm cuộc sống lấy kinh nghiệm ngoài sách vở, sinh viên sư phạm đi gia sư, làm thêm trong các trung tâm nên ra trường dễ dàng tìm được một công việc như ý muốn. Ngược lại, có những sinh viên xuất sắc, tốt nghiệp loại giỏi nhưng do chỉ có kiến thức lí thuyết, thiếu kinh nghiệm thực tế nên vẫn thất nghiệp. Những sinh viên chỉ mải tìm việc làm từ thực tế để tăng thu nhập mà không chú tâm rèn luyện lí thuyết để vận dụng đúng cũng thất bại trong việc tìm kiếm cơ hội việc làm tốt cho mình. Đó alf minh chứng cho sự đúng đắn của câu tục ngữ.
Vậy làm sao để chúng ta làm tốt được cả “học” và “hành”? Thiết nghĩ, một người cần hiểu rõ ràng mục đích và tầm quan trong của “học” đối với “hành” và ngược lại. Nhận thức đúng đắn điều này để chúng ta có sự cân bằng giữa hai yếu tố. Trong học tập lí thuyết trên lớp, cần cố gắng trau dồi lắng nghe, tuy nhiên cần cố gắng vận dụng những gì chúng ta đã học trong cuộc sống để giải quyết vấn đề, cần hiểu việc vận dụng phải linh hoạt và sáng tạo mới có hiệu quả tốt nhất.
“Học đi đôi với hành”, câu tục ngữ từ rất xa xưa nhưng đã thể hiện nhận thức đúng đắn từ rất sớm của ông cha ta về mối quan hệ giữa học và hành. Mỗi học sinh đang ngồi trên ghế nhà trường hãy luôn tâm niệm câu tục ngữ như một kim chỉ nam cho bản thân mình để học tập và ứng dụng một cách hiệu quả.
H
mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17
2
20 tháng 10 2021
Bài 6:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{41}=\dfrac{b}{29}=\dfrac{c}{30}=\dfrac{a+b}{41+29}=\dfrac{700}{70}=10\)
Do đó: a=410; b=290; c=300
1N
2
23 tháng 5 2022
Điện trở đèn:
\(R=\dfrac{U^2}{P}=\dfrac{12^2}{6}=24\Omega\)
Hai điện trở \(R_2;R_3\) mắc song song nhau\(\Rightarrow R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{20\cdot20}{20+20}=10\Omega\)
Điện trở tương đương:
\(R=R_Đ+R_{23}=24+10=34\Omega\)
Dòng điện qua mạch lúc này: \(I=\dfrac{U}{R}=\dfrac{15}{34}=0,44A\)
23 tháng 5 2022
b, Điển trở R1 của bóng đèn:
Từ công thức: \(P=\dfrac{U^2}{R}\Rightarrow R_1+\dfrac{U^2}{P}=12^2:6=24\Omega\)
Điện trở tương đương của đoạn mạch:
Vì R1 nt \(\left(R_2//R_3\right)\) nên \(R_{tđ}=R_1+\dfrac{R_2.R_3}{R_2+R_3}=24+\dfrac{20.20}{20+20}=34\Omega\)
Số chỉ của ampe kế: \(I=\dfrac{U}{R}=15:34=0,44A\)
H
8 tháng 8 2021
Bài 2 : (1) liên kết ; (2) electron ; (3) liên kết ; (4) : electron ; (5) sắp xếp electron
Bài 4 :
$\dfrac{M_X}{4} = \dfrac{M_K}{3} \Rightarrow M_X = 52$
Vậy X là crom,KHHH : Cr
Bài 5 :
$M_X = 3,5M_O = 3,5.16 = 56$ đvC
Tên : Sắt
KHHH : Fe
H
8 tháng 8 2021
Bài 9 :
$M_Z = \dfrac{5,312.10^{-23}}{1,66.10^{-24}} = 32(đvC)$
Vậy Z là lưu huỳnh, KHHH : S
Bài 10 :
a) $PTK = 22M_{H_2} = 22.2 = 44(đvC)$
b) $M_{hợp\ chất} = X + 16.2 = 44 \Rightarrow X = 12$
Vậy X là cacbon, KHHH : C
Bài 11 :
a) $PTK = 32.5 = 160(đvC)$
b) $M_{hợp\ chất} = 2A + 16.3 = 160 \Rightarrow A = 56$
Vậy A là sắt
c) $\%Fe = \dfrac{56.2}{160}.100\% = 70\%$
6 tháng 12 2021
Bài 12:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
31 tháng 10 2021
3: \(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
\(=6x^2-11x-35\)
4: \(\left(5x-2\right)\left(3x+4\right)\)
\(=15x^2+20x-6x-8\)
\(=15x^2+14x-8\)
D
5
AH
Akai Haruma
Giáo viên
19 tháng 1 2022
Bài 3:
a. $[25+(-15)]+(-25)=25-15-25=(25-25)-15=0-15=-15$
b. $512-(-88)-400-112$
$=512+88-400-112$
$=(512-112-400)+88=(400-400)+88=88$
c.
$-(310)+(-290)-907+107=-310-290-907+107$
$=-(310+290)-(907-107)=-600-600=-1200$
d.
$-2004-1975+2000-2025$
$=-(2004-2000)-(1975+2025)=-4-4000=-(4+4000)=-4004$
AH
Akai Haruma
Giáo viên
19 tháng 1 2022
Bài 1:
a. $ax+ay+bx+by=(ax+ay)+(bx+by)=a(x+y)+b(x+y)$
$=(x+y)(a+b)=17(-2)=-34$
b. $ax-ay+bx-by = (ax-ay)+(bx-by)$
$=a(x-y)+b(x-y)=(x-y)(a+b)=(-1)(-7)=7$
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
a.
ĐKXĐ: \(-3\le x\le\dfrac{3}{2}\)
Ta có:
\(4\sqrt{x+3}=2.2\sqrt{x+3}\le2^2+x+3=x+7\)
\(2\sqrt{3-2x}=2.1.\sqrt{3-2x}\le1^2+3-2x=4-2x\)
Do đó:
\(x+4\sqrt{x+3}+2\sqrt{3-2x}\le x+x+7+4-2x=11\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\sqrt{x+3}=2\\\sqrt{3-2x}=1\end{matrix}\right.\) \(\Leftrightarrow x=1\)
Vậy pt có nghiệm duy nhất \(x=1\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
b.
ĐKXĐ: \(x\ge-\dfrac{3}{2}\)
\(x^2+4x+5-2\sqrt{2x+3}=0\)
\(\Leftrightarrow\left(x^2+2x+1\right)+\left(2x+3-2\sqrt{2x+3}+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2+\left(\sqrt{2x+3}-1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=0\\\sqrt{2x+3}-1=0\end{matrix}\right.\)
\(\Leftrightarrow x=-1\)
Vậy pt có nghiệm duy nhất \(x=-1\)
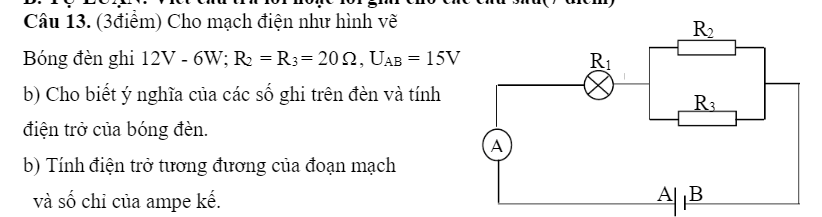
(Học sinh tự vẽ hình)
a. Chứng minh \(\bigtriangleup\)DGB và \(\bigtriangleup\)DEC, ta có:
DG = DE (gt)
BD = DC (gt)
\(\widehat{BDG}=\widehat{EDC}\)(đối đỉnh)
=>\(\bigtriangleup DGB = \bigtriangleup DEC\)
=> BG = EC (1)
Chứng minh tương tự, ta có \(\bigtriangleup\)BDE = \(\bigtriangleup\)GDC,
=> BE = GC (2)
Theo bài ra, ta có: G là trọng tâm tam giác ABC
=> BG = GC (3)
Từ (1), (2) và (3) suy ra: BG = GC = CE = EB
b. Xét \(\bigtriangleup ABE\) và \(\bigtriangleup ACE\), ta có:
AB = AC (gt)
BE = EC (cmt a)
AE cạnh chung
=> \(\bigtriangleup ABE = \bigtriangleup ACE\)