xét tính chẵn lẻ của hàm số \(\frac{\sqrt{2x+6}}{2x^2+4x+2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DV
đỗ văn thành
21 tháng 10 2016
Đúng(0)
Những câu hỏi liên quan
TV
1
5 tháng 2 2022
ĐKXĐ: \(\left\{{}\begin{matrix}5x+1>=0\\7-2x>0\end{matrix}\right.\Leftrightarrow-\dfrac{1}{5}\le x< \dfrac{7}{2}\)
Vậy: D=[-1/5;7/2)
Hàm số này không chẵn cũng không lẻ
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 10 2021
a. \(D=R\)
\(g\left(-x\right)=\sqrt{\left(-x\right)^4-2\left(-x\right)+3}-\sqrt{\left(-x\right)^4+2\left(-x\right)+3}\)
\(=\sqrt{x^4+2x+3}-\sqrt{x^4-2x+3}=-\left(\sqrt{x^4-2x+3}-\sqrt{x^4+2x+3}\right)\)
\(=-g\left(x\right)\)
Hàm lẻ
b.
\(D=R\)
\(h\left(-x\right)=\sqrt[3]{-x+1}-\sqrt[3]{-x-1}=-\sqrt[3]{x-1}+\sqrt[3]{x+1}\)
\(=\sqrt[3]{x+1}-\sqrt[3]{x-1}=h\left(x\right)\)
Hàm chẵn
HD
2
Y
16 tháng 10 2023
\(TXD\) \(D=R\backslash\left\{0\right\}\) là tập đối xứng.
\(\forall x\in D\Rightarrow-x\in D\)
Có \(f\left(-x\right)=\dfrac{\left(-x\right)^2+1}{\left|2\left(-x\right)+1\right|+\left|2\left(-x\right)-1\right|}\)
\(=\dfrac{x^2+1}{\left|1-2x\right|+\left|-2x-1\right|}\)
\(=\dfrac{x^2+1}{\left|-\left(2x-1\right)\right|+\left|-\left(2x+1\right)\right|}\)
\(=\dfrac{x^2+1}{\left|2x-1\right|+\left|2x+1\right|}\) \(=f\left(x\right)\)
Vậy hàm số \(y=f\left(x\right)=\dfrac{x^2+1}{\left|2x+1\right|+\left|2x-1\right|}\) là hàm số chẵn.
16 tháng 10 2023
TXĐ: D=R
Khi \(x\in D\) thì \(-x\in D\)
\(f\left(-x\right)=\dfrac{\left(-x\right)^2+1}{\left|-2x+1\right|+\left|-2x-1\right|}\)
\(=\dfrac{x^2+1}{\left|2x+1\right|+\left|2x-1\right|}=f\left(x\right)\)
=>f(x) chẵn
NT
1
18 tháng 10 2021
\(f\left(-x\right)=\left(-x\right)^{2020}-2\cdot\left(-x\right)^2-3\)
\(=x^{2020}-2x^2-3\)
=f(x)
=> f(x) là hàm số chẵn
BD
1
HP
12 tháng 12 2020
a, \(y=f\left(x\right)=2x^2+1\)
\(f\left(-x\right)=2x^2+1=f\left(x\right)\Rightarrow\) Là hàm chẵn
b, \(y=f\left(x\right)=5x^3-2x\)
\(f\left(-x\right)=-5x^3+2x=-f\left(x\right)\Rightarrow\) Là hàm lẻ
c, \(y=f\left(x\right)=\sqrt{x-1}\)
ĐK: \(x\ge1\)
\(-f\left(x\right)=-\sqrt{x-1}\ne f\left(x\right)\Rightarrow\) Không phải là hàm số chẵn, lẻ
d, \(y=f\left(x\right)=5x^2-\dfrac{1}{x}\)
ĐK: \(x\ne0\)
\(f\left(-x\right)=5x^2+\dfrac{1}{x}\ne f\left(x\right)\)
\(-f\left(x\right)=-5x^2+\dfrac{1}{x}\ne f\left(-x\right)\)
\(\Rightarrow\) Không phải là hàm số chẵn, lẻ
PT
1
CM
25 tháng 8 2018
Đồ thị là hình 26. Hàm số không là hàm số chẵn, không là hàm số lẻ
CM
15 tháng 1 2017
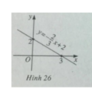
Đáp án D
Ta có tập xác định D = R.
Hàm số y = f(x) = 0 có:
f(-x) = 0 và –f(x) = 0
=> f(x) = f(-x) = -f(x) vừa thỏa mãn tính chất của hàm số chẵn, vừa thỏa mãn tính chất của hàm số lẻ, nên đây là hàm số vừa chẵn vừa lẻ.