cho hình bình hành ABCD có AD=4 và chiều cao tường ứng với cạnh AD bằng 3, \(\widehat{BAD}=60^0\) . Chọn hệ trục tọa độ \(\left(A;\overrightarrow{i};\overrightarrow{j}\right)\) sao cho \(\overrightarrow{i}\) cùng hướng với \(\overrightarrow{AD}\). Tìm tọa độ các vectơ \(\overrightarrow{AB};\overrightarrow{BC};\overrightarrow{CD};\overrightarrow{AC}\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài cạnh AD, DC của hình bình hành ABCD là a(cm) và b(cm)
Chu vi hình bình hành ABCD là: 2a+2b=70
\(2\times\left(a+b\right)=70\)
a+b=70:2
a+b=35 (1)
Lại có, cạnh đáy DC lớn hơn cạnh bên AD là 5cm: b-a=5 (cm)
b=5+a (2)
Thay (2) vào (1) ta được: a+5+a=35
2a=35-5
2a=30
a=30:2
a=15 (cm)
Vậy độ dài cạnh AD là 15 cm, độ dài cạnh DC là 15+5=20 cm
Diện tích hình bình hành ABCD là: \((2\times20\times9):2\)=180 cm2

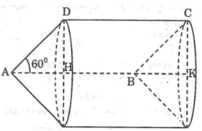
*Khi quay hình bình hành ABCD một vòng quanh cạnh AB thì cạnh AD và BC vạch nên hai hình nón bằng nhau có đường sinh AD = BC = x, cạnh CD vạch nên hình trụ có bán kính đáy bằng bán kính hình nón
Trong tam giác AHD,ta có:
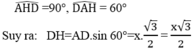
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
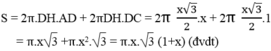
*Khi quay hình bình hành ABCD một vòng quanh AD thì cạnh AB và DC vạch nên hai hình nón bằng nhau có đường sinh AB = DC = 1, cạnh BC vạch nên hình trụ có bán kính đáy bằng bán kính đáy của hình nón
Ta có:
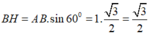
Diện tích toàn phần của hình tạo thành bằng tổng diện tích xung quanh của hai hình nón và diện tích xung quanh của hình trụ
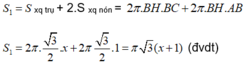

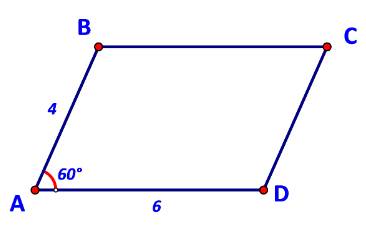
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)

Bn đang thi à
vậy thì bn phải tự làm nhỡ bn đi học lại bn lại vào bài này bn ko biết làm thì sao

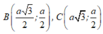
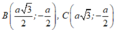
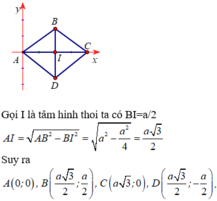
2