Chứng minh định nghĩa hay góc đối đỉnh thì bằng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
15 tháng 10 2021
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{BOD}+\widehat{AOD}=180^0\)
Do đó: \(\widehat{AOC}=\widehat{BOD}\)
DT
1
21 tháng 10 2021
AOC+ˆAOD=1800AOC^+AOD^=1800
ˆBOD+ˆAOD=1800BOD^+AOD^=1800
Do đó: ˆAOC=ˆBOD
NV
1
8 tháng 11 2015
xét các tia x'ox và y'oy, có hai góc đối đỉnh là xoy và x'oy'
gọi ot và ot' là hai tia phân giác tương ứng
Thấy: góc xoy = góc x'oy'
=> góc yot = góc y'ot'
ta có: góc xoy + góc xoy' = góc toy' + góc yot = 180o
<=> góc toy' + góc y'ot' = góc tot' = 180o
=> ot và ot' là hài tia đối nhau
7 tháng 9 2015
Giả Thiết 2 góc đối đỉnh Kết Luận Thì bằng nhau
IM
3 tháng 10 2016
O 1 2 3
| Giả thiết | Góc O1 và góc O3 đối đỉnh |
| Kết luận | Góc O1 = Góc O3 |
C/m :
Ta có :
\(\begin{cases}\widehat{O_1}+\widehat{O_2}=180^0\\\widehat{O_3}+\widehat{O_2}=180^0\end{cases}\) ( kề bù )
\(\Rightarrow\begin{cases}\widehat{O_1}=180^0-\widehat{O_2}\\\widehat{O_3}=180^0-\widehat{O_2}\end{cases}\)
\(\Rightarrow\widehat{O_1}=\widehat{O_3}\left(đpcm\right)\)
3 tháng 8 2015
GT KL đường thẳng a;b cắt nhau tại O góc O 1 và O 2 đối đỉnh góc O góc O 1 = 2 a b O 1 2 3
Vì góc O1 và góc O2 kề bù => O1 + O2 = 180o
Góc góc O2 và góc O3 kề bù => O2 + O3 = 180o
=> O1 = O2
CM
25 tháng 3 2017
Xác định câu đúng, sai trong các câu sau:
a) Hai góc đối đỉnh thì bằng nhau. Đ
b) Hai góc bằng nhau thì đối đỉnh. S
c) Hai góc có chung đỉnh và bằng nhau là hai góc đối đỉnh. S
d) Hai góc không đối đỉnh thì không bằng nhau. S
e) Hai góc không bằng nhau thì không đối đỉnh. Đ
17 tháng 9 2023
a)
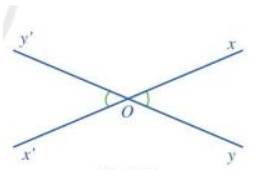
b)
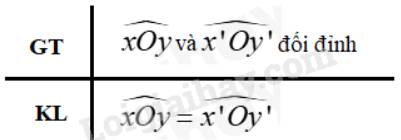
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)
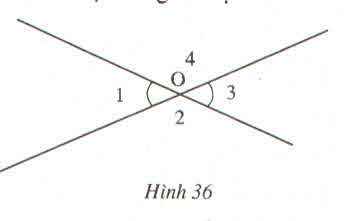
O y y' x x' 1 3 2 4
Ta có: O1+ O2 = 180o (hai góc kề bù)
O3 + O2 = 180o (hai góc kề bù)
=> O1 + O2 = O2 + O3
Vậy O1 = O3 ( O1 và O3 là hai góc đối đỉnh)