Cần gấp lắm rồi 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



S BCD=S DHB+S DHC
=1/2*HD*HB+1/2*HD*HC
=1/2*HD*12=6*HD
=6*1/3*AH=2AH
S ABH=1/2*BH*AH=1/2*4*AH=2AH
=>S ABH=S DBC

1: CN=3/5AC
=>S BNC/S BAC=3/5
=>S BNC=490*3/5=294cm2
2: EC=1/4BC
=>S AEC=1/4*S ABC
=>S ABC=4*117=468m2

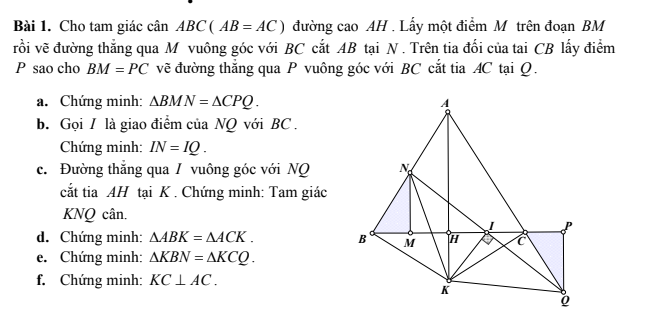
a, Vì tam giác ABC cân tại A nên \(\widehat{NBM}=\widehat{ACB}\)
Mà \(\widehat{ACB}=\widehat{PCQ}\left(đối.đỉnh\right)\Rightarrow\widehat{NBM}=\widehat{PCQ}\)
Mà \(\widehat{NMB}=\widehat{CPQ}=90^0;BM=PC\)
Do đó \(\Delta BMN=\Delta CPQ\left(g.c.g\right)\)
b, Vì \(BM//PQ\left(\perp BP\right)\) nên \(\widehat{MNI}=\widehat{IQP}\)
Mà \(\widehat{NMI}=\widehat{IPQ}=90^0;MN=PQ\left(\Delta BMN=\Delta CPQ\right)\)
Do đó \(\Delta IMN=\Delta IPQ\left(g.c.g\right)\)
\(\Rightarrow IN=IQ\)
c, Vì IK là đường cao cũng là trung tuyến tam giác KNQ nên tam giác KNQ cân tại K

Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(AB^2+AD^2=BD^2\)
\(\Leftrightarrow BD^2=6^2+8^2=100\)
hay BD=10(cm)
Ta có: ABCD là hình chữ nhật
mà O là giao điểm của hai đường chéo AC và BD
nên O là trung điểm chung của AC và BD
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAD vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(AH\cdot BD=AB\cdot AD\)
\(\Leftrightarrow AH=4.8\left(cm\right)\)
Ta có: ΔABD vuông tại A
mà AO là đường trung tuyến ứng với cạnh huyền BD
nên \(AO=\dfrac{BD}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAHO vuông tại H, ta được:
\(AO^2=AH^2+HO^2\)
\(\Leftrightarrow HO^2=5^2-4.8^2=1.96\)
hay HO=1,4(cm)
Diện tích tam giác AHO là:
\(S_{AHO}=\dfrac{HA\cdot HO}{2}=\dfrac{1.4\cdot4.8}{2}=3.36\left(cm^2\right)\)

a, \(2y^2\left(8y^6\right)y=16y^9\)
b, \(=\dfrac{3}{4}x^3y^4\)
c, \(=10x^3y^4z^8\)
d, \(=\left(\dfrac{3}{4}x^2y^3\right)\left(\dfrac{12}{5}x^4\right)=\dfrac{9}{5}x^6y^3\)
e, \(=-\dfrac{5}{4}x^5y^{10}\)
f, \(=120x^4y^6z^4\)

Bài 4:
45 phút=3/4 giờ
Bài 5:
x+3/10=-2/5
=>x=-2/5-3/10=-7/10
Bài 6:
\(=\dfrac{3^9\cdot5^{11}\left(5-3^2\right)}{5^{10}\cdot3^{10}}=\dfrac{5\cdot\left(-4\right)}{3}=-\dfrac{20}{3}\)






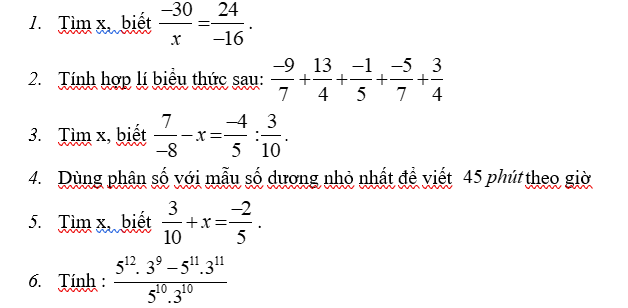 Giúp với ạ cần gấp lắm sắp thi rồi!!!!!!!!!!!!!!
Giúp với ạ cần gấp lắm sắp thi rồi!!!!!!!!!!!!!!
Giải:
Ta có: \(\frac{a}{2}=\frac{b}{3}\Rightarrow\frac{a}{10}=\frac{b}{15}\)
\(\frac{b}{5}=\frac{c}{4}\Rightarrow\frac{b}{15}=\frac{c}{12}\)
\(\Rightarrow\frac{a}{10}=\frac{b}{15}=\frac{c}{12}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{10}=\frac{b}{15}=\frac{c}{12}=\frac{a-b+c}{10-15+12}=\frac{-49}{7}=-7\)
+) \(\frac{a}{10}=-7\Rightarrow a=-70\)
+) \(\frac{b}{15}=-7\Rightarrow b=-105\)
+) \(\frac{c}{12}=-7\Rightarrow c=-84\)
Vậy a = -70, b = -105, c = -84
\(\frac{a}{2}=\frac{b}{3}\Rightarrow\frac{a}{10}=\frac{b}{15}\) (1)
\(\frac{b}{5}=\frac{c}{4}\Rightarrow\frac{b}{15}=\frac{c}{12}\) (2)
Từ (1) và (2)
\(\Rightarrow\frac{a}{10}=\frac{b}{15}=\frac{c}{12}\)
Áp dụng tích chất dãy tỉ số bằng nhau
\(\Rightarrow\frac{a-b+c}{10-15+12}=\frac{-49}{7}=-7\)
\(\frac{a}{10}=-7\Rightarrow a=-70\)
\(\frac{b}{15}=-7\Rightarrow b=-119\)
\(\frac{c}{12}=-7\Rightarrow c=-84\)
Vậy a=-70
b=-119
c=-84