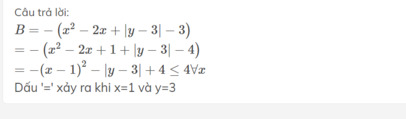Tìm GTLN của A=3-x^2+2X-(y-3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
3 tháng 2 2022
Đúng(0)
Những câu hỏi liên quan
EC
19 tháng 9 2016
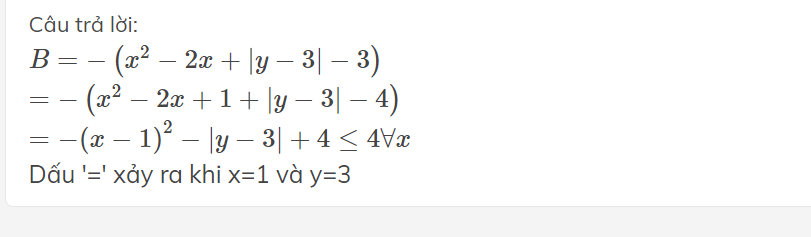
A=3-x2+2x-|y−3|
A=4-(x2-2x+1)-|y-3|
A=4-(x-1)2-|y-3|
Vì \(-\left(x-1\right)^2\le0;-\left|y-3\right|\le0\)
Suy ra:\(4-\left(x-1\right)^2- \left|y-3\right|\le4\)
Dấu = xảy ra khi x-1=0;x=1
y-3=0;y=3
Vậy Max A=4 khi x=1;3
6 tháng 1 2021
a) Ta có: \(Q=-x^2-y^2+4x-4y+2=-\left(x^2+y^2-4x+4y-2\right)\)
\(=-\left(x^2-4x+4+y^2+4y+4\right)+10\)
\(=-\left[\left(x-2\right)^2+\left(y+2\right)^2\right]+10\le10\forall x,y\)
Vậy MaxQ=10 khi x=2, y=-2
b) +Ta có: \(A=-x^2-6x+5=-\left(x^2+6x-5\right)=-\left(x^2+6x+9-14\right)\)
\(=-\left(x^2+6x+9\right)+14=-\left(x+3\right)^2+14\le14\forall x\)
Vậy MaxA=14 khi x=-3
+Ta có: \(B=-4x^2-9y^2-4x+6y+3=-\left(4x^2+9y^2+4x-6y-3\right)\)
\(=-\left(4x^2+4x+1+9y^2-6y+1-5\right)\)
\(=-\left[\left(2x+1\right)^2+\left(3y-1\right)^2\right]+5\le5\forall x,y\)
Vậy MaxB=5 khi x=-1/2, y=1/3
c) Ta có: \(P=x^2+y^2-2x+6y+12=x^2-2x+1+y^2+6y+9+2\)
\(=\left(x-1\right)^2+\left(y+3\right)^2+2\ge2\forall x,y\)
Vậy MinP=2 khi x=1, y=-3
N
2 tháng 12 2018
1) \(A=\frac{2018x^2-2.2018x+2018^2}{2018x^2}=\frac{\left(x-2018\right)^2+2017x^2}{2018x^2}=\frac{\left(x-2018\right)^2}{2018x^2}+\frac{2017}{2018}\)
vì \(\frac{\left(x-2018\right)^2}{2018x^2}\ge0\Rightarrow\frac{\left(x-2018\right)^2}{2018x^2}+\frac{2017}{2018}\ge\frac{2017}{2018}\)
dấu = xảy ra khi x-2018=0
=> x=2018
Vậy Min A=\(\frac{2017}{2017}\)khi x=2018
2) \(B=\frac{3x^2+9x+17}{3x^2+9x+7}=\frac{3x^2+9x+7+10}{3x^2+9x+7}=1+\frac{10}{3x^2+9x+7}=1+\frac{10}{3.x^2+9x+7}\)
\(=1+\frac{10}{3.\left(x^2+9x\right)+7}=1+\frac{10}{3.\left[x^2+\frac{2.x.3}{2}+\left(\frac{3}{2}\right)^2\right]-\frac{9}{4}+7}=1+\frac{10}{3.\left(x+\frac{9}{2}\right)^2+\frac{1}{4}}\)
để B lớn nhất => \(3.\left(x+\frac{3}{2}\right)^2+\frac{1}{4}\)nhỏ nhất
mà \(3.\left(x+\frac{3}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}\)vì \(3.\left(x+\frac{3}{2}\right)^2\ge0\)
dấu = xảy ra khi \(x+\frac{3}{2}=0\)
=> x=\(-\frac{3}{2}\)
Vậy maxB=\(41\)khi x=\(-\frac{3}{2}\)
3) \(M=\frac{3x^2+14}{x^2+4}=\frac{3.\left(x^2+4\right)+2}{x^2+4}=3+\frac{2}{x^2+4}\)
để M lớn nhất => x2+4 nhỏ nhất
mà \(x^2+4\ge4\)(vì x2 lớn hơn hoặc bằng 0)
dấu = xảy ra khi x2 =0
=> x=0
Vậy Max M\(=\frac{7}{2}\)khi x=0
ps: bài này khá dài, sai sót bỏ qua =))
OC
1
NT
22 tháng 9 2016
\(A=3-x^2+2x-\left|y-3\right|=-\left(x^2-2x+1\right)+4-\left|y-3\right|=-\left[\left(x-1\right)^2+4-\left|y-3\right|\right]\)
Mà : \(\begin{cases}\left(x-1\right)^2\ge0\\\left|y-3\right|\ge0\end{cases}\)
\(\Rightarrow\left(x-1\right)^2+\left|y-3\right|\ge0\\ \Rightarrow-\left[\left(x-1\right)^2+\left|y-3\right|\right]\le0\\ \Rightarrow A\le4\)
Dấu "=" xảy ra khi x=1;y=3
Vậy MAx A có GTLN khi x=1;y=3
DA
0