Tứ giác ABCD, A';B';C';D' là trọng tâm của các tam giác BCD, tam giác ACD, tam giác ABD, tam giác ABC. Chứng minh 4 đường thẳng AA';BB';CC';DD' đồng quy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^0\)

a) Xét tam giác ABC có
M là trung điểm của AB
N là trung điểm của BC
=>MN là đường tb của yam giác ABC
=>MN//AC và MN=1/2 BC (1)
cm tg tự => QP//AC và QP =1/2 AC (2)
Từ (1) và (2) => MNPQ là hbh
cho tứ giác ABCD có M,N,P,Q lần lượt là trung điểm của AB.BC,CD,DA
tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình vuông

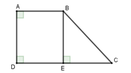
Vì A ^ = D ^ = 90 0 => AD // BC hay ABCD là hình thang vuông tại A, D
Kẻ BE ⊥ DC tại E
Tứ giác ABED có ba góc vuông A ^ = D ^ = E ^ = 90 o nên ABED là hình chữ nhật
Suy ra DE = AB = 6cm; BE = AD = 8cm
Xét tam giác BEC vuông tại E có B C E ^ = 45 0 nên tam giác BEC vuông cân tại E
EC = BE = 8cm DC = DE + EC = 6 + 8 = 14cm
Do đó:
SABCD = A B + C D . A D 2 = 6 + 14 8 2 = 80 c m 2 .
Đáp án cần chọn là: B