Cho tam giác ABC có AB = AC, trên nửa mặt phẳng có bờ là AB không chứa điểm C lấy điểm M sao cho góc BAM = góc B và AM = AB. Trên nửa mặt phẳng có bờ là AC không chưa điểm B lấy điểm N sao cho góc CAN = góc C. Từ A kẻ đường thẳng d vuông góc với BC
CMR: d là đường trung trực của MN

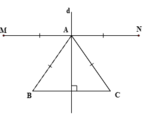
Ta có hình vẽ:
Ta có:
góc MAB = góc ABC mà MAB và ABC ở vị trí so le trong => AM // BC (1)
góc NAC = góc ACB mà NAC và ACB ở vị trí so le trong => AN // BC (2)
Từ (1) và (2) mà theo tiên đề Ơ-clit qua 1 điểm nằm ngoài 1 đường thẳng chỉ kẻ được đúng 1 đường thẳng song song với đường thẳng ban đầu => MA trùng với NA hay 3 điểm A, M, N thẳng hàng
=> MN // BC
Mà d vuông góc với BC, MN // BC => MN vuông góc với d (quan hệ từ vuông góc -> song song) (2)
Mặt khác, AM = AB, AB = AC, AC = AN
=> AM = AN hay A là trung điểm của MN (3)
Từ (2) và (3) => d là đường trung trực của MN (đpcm)