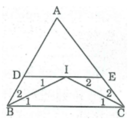
cho ΔABC, các tia phân giác của \(\widehat{B}\)và \(\widehat{C}\)cắt nhau tại I qua I kẻ đường thẳng song song với BC cắt AB và ac tại D và E
a) tìm các hình thang có trong hình.
b) Chứng minh hình thang BDCE có một cạnh đáy bằng tổng hai cạnh bên.
Mấy bạn giải hộ mình với ( Vẽ cả hình nữa nhé) ![]()