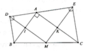
Cho tứ giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB(DA=DB) và ACE(EA=EC). Gọi M là trung điểm BC, I là giao điểm của DM với AB, K là giao điểm của EM với AC.Chứng minh
a, Ba điểm D,A,E thẳng hàng
b,Tứ giác IAKM là hình chữ nhật
c,Tam giác DME là tam giác vuông cân

a) Ta có A1 + C1 = 90 độ (...)
A3 + B1 = 90 độ (...)
=> A1 + A3 + C1 + B1 = 180 độ (1)
Có BD vuông góc DE
CE vuông góc DE
=> BD // EC
=> B1 + B2 + C2 + C1 = 180 độ
Mà B2 + C2 = 90 độ => B1 + C1 = 90 độ (2)
Từ (1) và (2) => A3 + A1 = 90 độ. Mà A2 = 90 độ
Suy ra : A1 + A2 + A3 = 180 độ. Hay góc DAE là góc bẹt
=> D,A,E thẳng hàng.
b) Ta có AM=MC
AE=EC
=> ME là đường trung trực của AC.
=> AKM = 90 độ (3)
CMTT => AIM = 90 độ (4)
Mà IAK = BAC = 90 độ (5)
Từ (3)(4)(5) => IMKA là hình chữ nhật
c) Có ME là đường trung trực của AC (câu b)
Mà ▲AEC vuông cân tại E => EM là tia phân giác AEC
=> AEM = 90/2 = 45 độ. (*)
Ta lại có IMKA là hình chữ nhật => IMK = 90 độ (**)
Từ (*) và (**) => ▲DME vuông cần tại M
đúng ko vậy