cho ▲ABC. CM: \(\frac{sinA}{2}.\frac{sinB}{2}.\frac{sinC}{2}\le\frac{1}{8}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AL
cho tam giác ABC, chứng minh rằng: \(sinA+sinB-sinC=4.sin\frac{A}{2}.sin\frac{B}{2}.cos\frac{C}{2}\)
1
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2019
\(sinA+sinB-sinC=2sin\frac{A+B}{2}cos\frac{A-B}{2}-sinC\)
\(=2cos\frac{C}{2}.cos\frac{A-B}{2}-2sin\frac{C}{2}cos\frac{C}{2}\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}-sin\frac{C}{2}\right)\)
\(=2cos\frac{C}{2}\left(cos\frac{A-B}{2}-cos\frac{A+B}{2}\right)\)
\(=4cos\frac{C}{2}sin\frac{A}{2}sin\frac{B}{2}\)
2 tháng 2 2022
Tham khảo:
Chứng minh định lý hàm cos
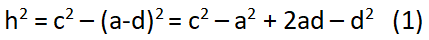
Chứng minh định lý hàm cos – Phương trình 1
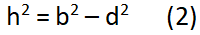
Chứng minh định lý hàm cos – Phương trình 2
Chứng minh định lý hàm cos – Phương trình 3
Với d = b cosC thế vào phương trình biến đổi (3) ta rút ra điều phải chứng minh!
10 tháng 9 2016
A B C A' C' B' H a b c
\(AA'=c.sinB=b.sinC\Leftrightarrow\frac{c}{sinC}=\frac{b}{sinB}.\)
va\(BB'=c.sinA=a.sinC\Leftrightarrow\frac{c}{sinC}=\frac{a}{sinA}\)
\(\Leftrightarrow\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\)
\(S_{\Delta ABC}=\frac{1}{2}.a.AA'=\frac{1}{2}.a.bsinC\)
N
2
8 tháng 11 2017
Câu hỏi của lê thị thu huyền - Toán lớp 9 - Học toán với OnlineMath
TP
1. cho tam giác abc nhọn có AB=c , AC=b , BC=a
c/m : \(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}\)
1
26 tháng 7 2015
A B C H
Kẻ đường cao AH vuông góc với BC (H \(\in\) BC)
Xét tam giác AHB vuông tại H ta có: \(\sin B=\frac{AH}{c}\Leftrightarrow AH=sinB\times c\) (1)
Xét tam giác AHC vuông tại H ta có: \(\sin C=\frac{AH}{b}\Leftrightarrow AH=\sin C\times b\) (2)
(1),(2)\(\Rightarrow\sin C\times b=\sin B\times c\Leftrightarrow\frac{b}{\sin B}=\frac{c}{\sin C}\)
Rồi bạn chứng minh tương tự nha!