Giúp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
Gọi số học sinh là x
Theo đề, ta có: \(x-5\in BC\left(8;12;15\right)\)
mà 300<=x<=400
nên x=365

a)\(-1,6:\left(1+\dfrac{2}{3}\right)=-1,6:\dfrac{5}{3}=-\dfrac{8}{5}.\dfrac{3}{5}=\dfrac{-24}{25}\)
b)\(\left(\dfrac{-2}{3}\right)+\dfrac{3}{4}-\left(-\dfrac{1}{6}\right)+\left(\dfrac{-2}{5}\right)=-\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{1}{6}-\dfrac{2}{5}=\dfrac{-40+45+10-24}{60}=\dfrac{-9}{60}=\dfrac{-3}{20}\)
c)\(\left(\dfrac{-3}{7}:\dfrac{2}{11}+\dfrac{-4}{7}:\dfrac{2}{11}\right).\dfrac{7}{33}=\left(\dfrac{-3}{7}.\dfrac{11}{2}+\dfrac{-4}{7}.\dfrac{11}{2}\right).\dfrac{7}{33}=\left[\dfrac{11}{2}\left(\dfrac{-3}{7}+\dfrac{-4}{7}\right)\right].\dfrac{7}{33}=\dfrac{-11}{2}.\dfrac{7}{33}=\dfrac{-7}{6}\)
d)\(\dfrac{-5}{8}+\dfrac{4}{9}:\left(\dfrac{-2}{3}\right)-\dfrac{7}{20}.\left(\dfrac{-5}{14}\right)=\dfrac{-5}{8}-\dfrac{4}{9}.\dfrac{3}{2}+\dfrac{1}{8}=\dfrac{-5}{8}+\dfrac{1}{8}-\dfrac{2}{3}=-\dfrac{7}{6}\)

Christmas is a magical and enchanting time of year. It is a joyous and festive occasion filled with love, happiness, and excitement. The air is filled with a warm and cozy atmosphere, as families come together to celebrate. The beautifully decorated Christmas tree sparkles with twinkling lights and shimmering ornaments. Delicious and indulgent feasts are prepared, filling the air with mouth-watering aromas. Generosity and kindness abound as people exchange thoughtful and heartfelt gifts. The joyful laughter of children fills the air, accompanied by the melodic sounds of Christmas carols. The winter scenery is breathtaking, with glistening snowflakes and frosty landscapes. The spirit of Christmas is truly magical, bringing warmth, joy, and togetherness to all.
Christmas is a magical and enchanting time of year. It is a joyous and festive occasion filled with love, happiness, and excitement. The air is filled with a warm and cozy atmosphere, as families come together to celebrate. The beautifully decorated Christmas tree sparkles with twinkling lights and shimmering ornaments. Delicious and indulgent feasts are prepared, filling the air with mouth-watering aromas. Generosity and kindness abound as people exchange thoughtful and heartfelt gifts. The joyful laughter of children fills the air, accompanied by the melodic sounds of Christmas carols. The winter scenery is breathtaking, with glistening snowflakes and frosty landscapes. The spirit of Christmas is truly magical, bringing warmth, joy, and togetherness to all.



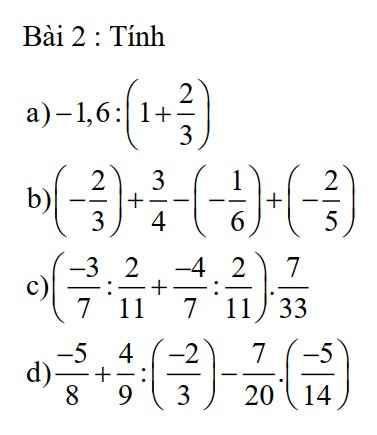 giúp với giúp với giúp e với ạ. e cảm ơn
giúp với giúp với giúp e với ạ. e cảm ơn


Ta có : \(\frac{1}{\left(x+1\right)^2}+\frac{x+1}{8}+\frac{x+1}{8}\ge3.\sqrt[3]{\frac{1}{\left(x+1\right)^2}.\frac{\left(x+1\right)^2}{64}}=\frac{3}{4}\)
\(\Rightarrow\frac{1}{\left(x+1\right)^2}\ge\frac{3}{4}-\frac{x+1}{4}\)
Tương tự , ta có : \(\frac{1}{\left(y+1\right)^2}\ge\frac{3}{4}-\frac{y+1}{4}\) ; \(\frac{1}{\left(z+1\right)^2}\ge\frac{3}{4}-\frac{z+1}{4}\)
Cộng các bđt trên với nhau : \(A\ge\frac{3}{4}.3-\frac{x+y+z+3}{4}\ge\frac{9}{4}-\frac{3\sqrt[3]{xyz}+3}{4}=\frac{3}{4}\)
Vậy Min A = 3/4 <=> x = y = z = 1